Subsections

• Introduction
• Background
• Problem 1: Radioactive Decay
  • Preliminary remarks
  • Exercise
• Problem 2:Logarithmic scale
  • Preliminary remarks
  • Exercise
• Problem 3: Newton's Law of Cooling
  • Preliminary remarks
  • Exercise
• Problem 4: Population Growth According to Malthus and
  Verhulst
  • Preliminary remarks
  • Exercise

Applications of Exponential and
Logarithmic Function

Introduction

The purpose of this lab is to familiarize you with some applications from real life involving exponential and logarithmic functions. The diversity of the processes which are described by the natural exponential function appears amazing. In this lab, you will encounter to three very different applications and try to use Maple to simplify computations and visualize behaviors of the processes in time.

The lab consists of Background including both the relevant theoretical notes and description of the use of appropriate Maple commands. There are four problems, each of which has separate preliminary remarks (discussion of equations, introduction of terms, etc.) and an exercise to do.

Background

Theoretical notes. In many natural processes the rate of change of physical quantity (temperature, velocity amount of money, electric current, whatever) is proportional to the current amount of the quantity. If we also know the amount present at time t=0, call it y₀, we can find y as a function of t by solving the following initial value problem:

Differential equation: 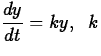$$\frac{dy}{dt} = ky,\;\; k$$ is a constant. (1)
Initial conditions: y = y₀ when t = 0 .

If y is positive and increasing, then k is positive, and we use Eq. (1) to say that the rate of growth is proportional to what has already been accumulated. If y is positive and decreasing, then k is negative, and Eq. (1) is used to say that the rate of decay is proportional to the amount still left.

It is seen that the constant function y = 0 is a solution of Eq. (1). To find the non-zero solutions, the equation is solved in accordance with the known technique of separating variables and integrating. The solution involves the natural exponential function (whose derivatives is the function itself) and is expressed as

The constant k is called the growth rate in exponential growth (k >0) and the decay rate in exponential decay (k < 0). In a process that can be modeled by exponential functions, the rate constant k depends only on the process and the conditions under which it is carried out.

Some processes are described by differential equations similar to (1) but containing two or more constants characterizing some other circumstances in which these processes are carried out. Also, the initial conditions might be specified by more complicated expressions. The corresponding initial value problems lead to the solution having slightly different form, e.g., like (2) including a combination of additive and multiplicative constants. You will meet illustrations of that in the problems below.

In some applications, a physical quantity varies on a huge range. To make this quantity more convenient to handle, special scales involving logarithms are used. This allows one to deal with the corresponding powers instead of actual values of y .

Relevant Maple Means. In order to enter the exponential and natural logarithmic functions, use the exp and ln command. The syntax of these commands is similar to that of sin and cos. For example, below it is shown how to enter the function f(x) = e^x and then evaluate it at x = 0.8.

  > f:=exp(x);

  > evalf(subs(x=0.8, f)); 

We suggest the commands involving expressions instead of functions here because they might be useful when doing exercises below.

In the same manner, the function $g(x) = \ln(x)$ is entered and calculated. Try the following commands:

  > g := ln(x);

  > evalf(subs(x=0.8, g));

To simplify expression involving logarithms, use command simplify; it works as follows:

  > simplify(exp(a+ln(b*exp(c))));

The common logarithm is defined by function log10 = log[10], but log10 must be defined with the command readlib(log10) before use:

  > readlib(log10): log10(10000);

Maple manipulates with common logarithms the same way but may return expressions including natural logarithms.

The solve command is usually sufficient for solving most problems encountered in your Calculus courses. This command comes in a couple of varieties, as shown below.

i.

Solve linear equation:

> solve (y=n*(x+1)-m(x-1),x);

ii.

Solve displaying result as an equation:

  > solve (5+7*x=39-10*x,x);

Plotting the two functions f(x) = e^x and $g(x) = \ln x$ on the same coordinate system illustrates an idea of the symmetry around the line y=x. All the three graphs can be plotted by the use of the following command:

  > plot({f,g,x}, x=-4..4, y=-4..4);   

Responding this command, Maple returns the figure as shown in Figure 1.

In order to get a graph of a left-hand/right-hand side of an equation obtained after symbolic transformations and/or computations, first use commands lhs and rhs respectively. The example:

  > eq1 := A=b+c*exp(k*t): eq2 := subs(b=2.5,c=3,k=0.8,eq1):

  > rh2 := rhs(eq2):

  > plot(rh2, t=0..3); 

When analyzing graphs obtained as the result of your computation, you may need to plot supplementary or auxiliary straight lines in the same figure. The following format of the plot command illustrates how the line y = 60 from x = 0 to x = 20 can be displayed:

  > plot({[0,60], [20,60]});

Problem 1: Radioactive Decay

Preliminary remarks

Radioactive decay is a typical example to which the exponential decay model can be applied. In Eq. (2), y represents the mass (in grams) of an isotope, y₀ and k are constants determining from initial conditions: y₀ is the mass present originally, and k is the decay constant.

k is often specified in terms of an empirical parameter, the half-life of the isotope. The half-life $\tau$ of a sample of a radioactive isotope is the time required for half of the atoms of that sample to decay. The half-lives of some common radioactive isotopes are as follows:

Uranium (U-238) 4,510,000,000 years

Plutonium (Pu-239) 24,360 years

Carbon (C-14) 5,730 years

Einsteinium (Es-254) 270 days

Nobelium (No-257) 23 sec

The relationship between k and $\tau$ is set up from the condition saying that the sample of y₀ grams will contain only $$\frac{1}{2}y_0$$ grams after the time $\tau$, so that, referring to equation (2):

and therefore:

The worst nuclear accident in history happened on April 26, 1986 at 01:23 a.m. (GMT +03:00) at the Chernobyl nuclear plant 60 miles north of Kiev in the Ukraine. An explosion destroyed one of the plant's four reactors, releasing large amount of radioactive isotopes into the atmosphere. For almost two weeks the radiation continued to escape and clouds settled onto villages, towns, and forests across wide stretches of Ukraine, Belarus, and neighboring parts of Russia. About 300,000 people were evacuated from the fallout areas. The estimate of the accident's ultimate death toll varies from several thousand to half a million deaths. (For more information, see `The Chernobyl Nuclear Accident'* site at Geocities.com)

* www.geocities.com/RainForest/Canopy/3643/chern.html

Exercise

Consider 20 grams of the plutonium isotope Pu-239 released in the Chernobyl nuclear accident.

1.

How long will it take for the 20 grams to decay to 5 grams?

2.

Plot the graph showing the decay of the mass of the plutonium isotope took place up to date (1986-1998). Does it look like a typical curve of exponential decay? Why? Discuss the graph in the context of the radioactive safety.

Problem 2:Logarithmic scale

Preliminary remarks

Base 10 logarithms, often called common logarithms, appear in many scientific and applied formulas.

For example, earthquake intensity is often reported on the logarithmic Richter scale. Here the formula is

where a is the amplitude of the ground motion in microns at the receiving station, T is the period of the seismic wave in seconds, and B is an empirical factor that allows for the weakening of the seismic wave with increasing distance from the epicenter of the earthquake. For an earthquake 10,000 km from the receiving station, B = 6.8. Thus if the recorded vertical ground motion is a = 10 microns and the period is T = 1 sec, the earthquake's magnitude, following (7), is R = 7.8. An earthquake of this magnitude does great damage near its epicenter.

Another example of the use of common logarithms is the decibel scale using, particularly, for measuring loudness. (The decibel unit is named in honor of Alexander G. Bell (1847-1922), inventor of the telephone.) If I is the intensity of sound in watts per square meter, the decibel level of the sound is

where I₀ is an intensity of 10^-12 watts per square meter corresponding roughly to the faintest sound that can be heard.

Exercise

When tuning the rock band's equipment before the concert in a big concert hall, an audio engineer finds that in order to maintain appropriate loudness in this hall, he needs to increase the power of the amplifiers compared with the level used for the previous concert in a smaller hall. Use formula (8)

(a)

to find what tripling the power adds to the level of loudness in decibels;

(b)

to determine by what factor k the engineer has to multiply the intensity of I of the sound to add 15 dB to the sound level S for the next concert of the band on the stadium.

Problem 3: Newton's Law of Cooling

Preliminary remarks

An aluminum beam brought from the outside cold into a machine shop where the regular normal temperature is maintained warms up to the temperature of the surrounding air. A hot silver ingot immersed in water cools to the temperature of the surrounding water.

In situations like these, the rate at which an object's temperature is changing at any given time is approximately proportional to the difference between its temperature and the temperature of the surrounding medium. This observation is sometimes called the Newton's Law of Cooling, although, as in the case with the aluminum beam, it applies to warming as well.

An equation representing this law is derived from a corresponding differential equation and can be written as

where T is the temperature of the object at time $t, \;T_s$ is the surrounding temperature, T₀ is the value of T when t = 0.

Exercise

A pot of mushroom soup taken from a microwave oven at $96^\circ$C and a jug of apple juice taken from a refrigerator at $4^\circ$C are put on a dinner table. The temperature in the dining room is held at $22^\circ$C. After 10 minutes, the soup temperature is $52^\circ$C and the juice temperature is $15^\circ$C.

1.

How much longer will it take the soup to lose its taste quality, i.e., to cool down to the temperature of $32^\circ$C? What is the juice temperature at this moment? When would the soup reach this temperature if it was left on a table of an outside cafe on a hot summer day when the temperature is $30^\circ$C? Why are the results so different?

2.

Plot the graphs T versus t for both products for the inside environment. Also, plot the graph of the functions representing the behavior of the surrounding temperature. Use the same coordinate axes. Analyze the graphs and come to a conclusion about what causes the difference in the graph's appearance.

3.

From the graphs, make an estimate when the soup should be eaten if it is supposed to be best at $65^\circ$C?

Problem 4: Population Growth According to Malthus and
Verhulst

Preliminary remarks

Thomas Robert Malthus (1766-1834), English economist and sociologist, was a pioneer in modern world population study. In An Essay on the Principle of Population (1798; rev. ed. 1803) he suggested that populations tend to increase exponentially, whereas resources which support populations (e.g., food) tend to grow only linearly. So poverty, distress, wars, famine are unavoidable because population increases faster than the means of subsistence.

The differential equation (1) may be regarded as a mathematical model of the changing population according to Malthus. Thus population P(t) with constant birth rate $\beta$ and constant death rate $\delta$ is given by

where P₀ = P(0) and $\mu = \beta - \delta$ is called the Malthusian parameter. If t is measured in years, it represents the annual growth rate, which, depending on the relationship between $\beta$ and $\delta$, can be positive, negative, or zero.

However, equation (3) describes only the simplest ideal situation, in which the inner impulse of the population to expand is given a completely free rein; it does not take into account any of the inhibiting factors that put a ceiling on the possible size of a real population. It is obvious, for example, that the human population of the earth can never expand to the stage where there will be only a small fraction of an acre of usable land per person. Long before the point is reached at which the whole surface of the earth becomes teeming slum, the rate of population growth will be forced down; social, psycological, and economic effects will depress the birth rate $\beta$ and increase the death rate $\delta$.

In about 1840 the Belgian mathematician Pierre-Francoise Verhulst proposed a population growth model which takes into account the possible limitation of population size due to limited resources. It is called logistic model. When the population P(t) is small, it tends to grow at a rate proportional to itself; but when it becomes larger, P(t) grows at a smaller rate. If L is the largest population beyond which the population cannot grow, the rate of growth of the population is assumed to be proportional to P and to (L - P), so that

The solution of equation (4) subject to the condition that P = P₀ when t = 0 is obtained by separation of variables and eventually yields

Since $\beta$ and $\delta$ depend on time, parameter k in (5) is interpreted as not their difference but rather as the maximum possible rate of population growth which is the net effect of birth and death rates.

Exercise

In accordance with some environmental and demographic studies, the earth will not support a population of more than 16 billion. It is also known that there were 2 billion people in 1925 and 4 billion people in 1975.

1.

Find the exact population in 2015 using both models. Plot graphs of both models. From the graphs, estimate when, following the Malthus exponential growth model, the population will reach 16 billion, and then estimate the size of the population in this year in accordance with the Verhulst logistic model.

2.

Compute when in accordance with the logistic model, the birth rate will be equal to the death rate, in other words, find the inflection point of the logistic graph.