Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for
![]()
![]()
![]()
Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
In this lab you will study a link between finding the area under the graph of a function and antidifferentiating the function.
In the following simple approximation schemes, the area under the curve and above each subinterval is approximated by the area of a rectangle, with the height of the rectangle being chosen according to some rule. The rules we will be concerned with are as follows.
The Maple student package has commands for visualizing these two rectangular area approximations. To use them, you first must load the student package via the with command. Then try the commands given below. Make sure you understand the differences between the two different rectangular approximations.
> with(student):
> f:=x-> x^2 ;
![]()
> rightbox(f(x),x=0..4);
> leftbox(f(x),x=0..4);
There are also Maple commands leftsum and rightsum to sum the areas of the rectangles, see the examples below. Note the use of evalf to obtain numerical answers.
> rightsum(f(x),x=0..4);
> evalf(rightsum(f(x),x=0..4));
> evalf(rightsum(x,x=0..2));
Unless specified, Maple will break the given interval into four subintervals. Below are some examples of how to change the number of subintervals used in the approximation.
> evalf(rightsum(x,x=0..2,10));
> evalf(rightsum(x,x=0..2,20));
> evalf(rightsum(x,x=0..2,100));
You have seen in lecture that the position p(t) of an object can be recovered from the velocity v(t) if one knows position at some particular time. This is done by antidifferentiating v(t). However, there is another way to think about recovering the position function, based on finding ``area'' under the velocity function.
Suppose v(t)=t2, p(0)=0, and you want to find p(1) (without knowing
calculus). How could you do this? First, just try to find a good
approximation of position at time 1. Notice that the only thing you really
know about finding position from velocity is that if velocity is constant (V)
and the object travels for time T, then the change in position
is V T. This can be used to approximate p(1) since if the time
interval [0,1] is divided into n subintervals, v(t) will be close to
a constant in each subinterval (for large enough n), and so the change in
position over a time interval of length ![]() is approximately
is approximately ![]() , where ti
is any particular time in our time interval. The total
change in position can then be approximated by
, where ti
is any particular time in our time interval. The total
change in position can then be approximated by
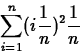
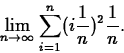
Christine Bonini