


Next: About this document ...
Up: No Title
Previous: No Title
Subsections
The purpose of this lab is to use Maple to study applications of
exponential and logarithmic functions. These are used to model many
types of growth and decay, as
well as in many scales, such as the Richter and decibel scales.
The simplest model for growth is
exponential, where
it is assumed that
y'(t) is proportional to y. That is,
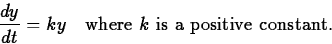
Separating the variables and integrating (see section 4.4 of the text),
we have
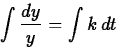
so that
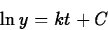
(If y is a positive quantity, we may drop the absolute value signs
around y.) Solving for y
y = ekt + C
which we may write in the form y = Aekt, where A is an arbitrary
positive constant.
In a sample of a radioactive material, the
rate at which atoms decay is proportional to the amount of material present.
That is,
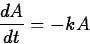
where k>0 is a constant. This is the same equation as in exponential growth,
except that -k replaces k. The solution is
A(t) = A0 e-kt
where A0 is a positive constant. Physically, A0 is the amount of
material present at t=0.
Radioactivity is often expressed in terms of an element's half-life.
For example, the half-life of carbon-14 is 5730 years. This statement means
that for any given sample of 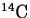 , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that 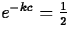 , so that
, so that 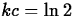 and
and 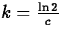 .
.
What is usually called Newton's law of cooling is a simple model for
the change in temperature of an object that is in contact with an
environment at a different temperature. It says that the rate of
change of the temperature of an object is proportional to the
difference between the object's temperature and the temperature of the
environment. Mathematically, this can be expressed as the differential
equation
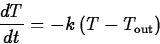
where k is the constant of proportionality and 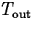 is
the temperature of the environment. Using a technique called
separation of variables it isn't hard to derive the solution
is
the temperature of the environment. Using a technique called
separation of variables it isn't hard to derive the solution
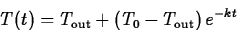
where T0 is the temperature of the object at t=0.
If a drug is adminstered to a patient intravenously, the concentration
jumps to its highest level almost immediately. The concentration
subsequently decays exponentially. If we use C(t)
to represent the concentration at time t, and C0 to represent the
concentration just after the dose is administered then our exponential
decay model would be given by
C(t) = C0 e-kt
A problem facing physicians is the fact that for most drugs, there is
a concentration, m, below which the drug is ineffective and a
concentration, M, above which the drug is dangerous. Thus the
physician would like the have the concentration C(t) satisfy
m < C(t) < M
This means that the initial dose must not produce a concentration
larger than M and that another dose will have to be administered
before the concentration reaches m.
The main functions you need are the natural exponential and
natural logarithm. The Maple commands for these functions are
exp and ln. Here are a few examples.
> f := x -> exp(-2*x);
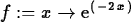
> simplify(ln(3)+ln(9));
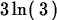
> ln(exp(x));
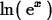
> simplify(ln(exp(x)));
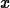
> solve(exp(-3*x)=0.5,x);
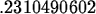
> plot(log[10](x),x=0..100);
Sometimes you need to use experimental data to determine the value of
constants in models. For example, suppose that for a particular drug,
the following data
were obtained. Just after the drug is injected, the concentration is
1.5 mg/ml (milligrams per milliliter). After four hours the
concentration has dropped to 0.25 mg/ml. From this data we can
determine values of C0 and k as follows. The value of C0 is the
initial concentration, so we have
C0 = 1.5
To find the value of k we need to solve the equation
0.25 = 1.5 e-4k
which we get by plugging in t=4 and using the data
C(4)=0.25. Maple commands for solving for k and defining and
plotting the function C(t) are shown below.
> k1 := solve(0.25=1.5*exp(-4*k),k);
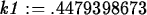
> C1 := t -> 1.5*exp(-k1*t);
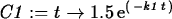
> plot(C1(t),t=0..6);
- 1.
- Suppose that b satisfies b > 1. Explain the relationship
between the graphs of
f(x) = bx
and
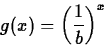
- 2.
- Suppose that the population of a certain bacteria can be modeled
by an exponential function. In a particular experiment, the number of
bacteria was 10,000 at t=0. Four hours later, the number of
bacteria was 250,000. Suppose a second experiment is performed under
the same conditions, but the number of bacteria at t=0 is only
2000. Show, using the equation for exponential growth, that the
predicted number of bacteria after four hours in this second
experiment is 50,000.
- 3.
- Suppose that for a certain drug, the following results were
obtained. Immediately after the drug was administered, the
concentration was 3.3 mg/ml. Six hours later, the concentration had
dropped to 1.55 mg/ml. Determine the value of k for this drug.
- 4.
- Suppose that for the drug in the previous exercise, the maximum
safe level is
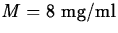 and the minimum effective level is
and the minimum effective level is
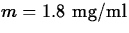 . What is the maximum possible time between doses
for this drug? (Hint - the initial dose should give an initial
concentration of C0 = M = 8.)
. What is the maximum possible time between doses
for this drug? (Hint - the initial dose should give an initial
concentration of C0 = M = 8.)
- 5.
- A thermometer is taken from a room at
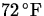 to the outdoors where the temperature is
to the outdoors where the temperature is 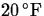 . Determine the reading on the thermometer after 5 minutes,
if the reading drops to
. Determine the reading on the thermometer after 5 minutes,
if the reading drops to 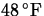 after 1 minute.
after 1 minute.



Next: About this document ...
Up: No Title
Previous: No Title
Jane E Bouchard
2/11/2000
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that ![]() , so that
, so that ![]() and
and ![]() .
. ![]()
![]()
![]()