


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to give you some experience with using the
trapezoidal rule and Simpson's rule to approximate integrals.
The trapezoidal rule and Simpson's rule are used for approximating area under a curve or the definite integral
Both methods start by dividing the interval ![$[a,b]$](img2.png) into
into 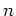 subintervals of equal length by choosing a partition
subintervals of equal length by choosing a partition
satisfying
where
is the length of each subinterval. For the trapezoidal rule, the
integral over each subinterval is approximated by the area of a
trapezoid. This gives the
following approximation to the integral
For Simpson's rule, the function is approximated by a parabola over
pairs of subintervals. When the areas under the parabolas are computed
and summed up, the result is the following approximation.
The commands for the trapezoidal rule and Simpson's rule are in the student package.
>with(student);
The following example will use the function
>f:=x->x^2*exp(x);
This computes the integral of the function from 0 to 2.
>int(f(x),x=0..2);
Using the evalf command provides a decimal approximation.
>evalf(int(f(x),x=0..2));
The command for using the trapezoidal rule is trapezoid. The syntax is very similar to that of the int command. the last argument specifies the number of subintervals to use. In the command below, the number of subintervals is set to 10, but you should experiment with increasing or decreasing this number.
Note that Maple writes out the sum and doesn't evaluate it to a number.
>trapezoid(f(x),x=0..2,10);
Putting an evalf command on the outside computes the trapezoidal approximation.
>evalf(trapezoid(f(x),x=0..2,10));
The command for Simpson's rule is very similar.
>simpson(f(x),x=0..2,10);
>evalf(simpson(f(x),x=0..2,10));
- For the function
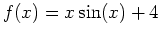 , use the trapezoidal rule formula to approximate the area under
, use the trapezoidal rule formula to approximate the area under 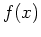 over the interval
over the interval ![$[0,4]$](img11.png) ising
ising 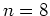 . Verify your answer using the trapezoid command in Maple. Repeat this exercise with simpson's rule.
. Verify your answer using the trapezoid command in Maple. Repeat this exercise with simpson's rule.
- Plot the function
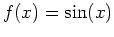 between
between 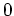 and
and 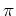 .
Using the trapezoid rule find the minimum number of subintervals necessary to approximate the area to within 0.001. Then do the same with Simpson's rule. Which rule is more accurate and why?
.
Using the trapezoid rule find the minimum number of subintervals necessary to approximate the area to within 0.001. Then do the same with Simpson's rule. Which rule is more accurate and why?
- There is an error term associated with the trapezoidal rule that can be used to estimate the error. More precisely, we have
where
for some value 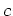 between
between 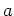 and
and 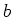 that maximizes the second derivative in absolute value. Solving the error formula for
that maximizes the second derivative in absolute value. Solving the error formula for 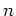 guarantees a number of subintervals such that the error term
guarantees a number of subintervals such that the error term 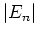 is less than some desired tolerance
is less than some desired tolerance 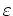 . This gives:
. This gives:
The way to think about this result is that it gives a value for 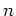 which guarantees that the error of the trapezoidal rule is less than the tolerance
which guarantees that the error of the trapezoidal rule is less than the tolerance 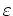 . It is generally a very conservative result.
For the function
. It is generally a very conservative result.
For the function
over the interval ![$[0,5]$](img25.png) , find the value of
, find the value of 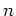 using the error estimate and see if the actual number of subintervals required to satisfy a tolerance of
using the error estimate and see if the actual number of subintervals required to satisfy a tolerance of
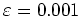 is smaller than the number given by the error estimate.
is smaller than the number given by the error estimate.
Similarly, the number of subintervals for the simpson rule approximation to guarantee an error smaller than 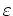 is
is
where 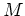 is the maximum of
is the maximum of
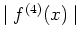 on the interval
on the interval
![$[a,b]$](img2.png) . Again, find the value of
. Again, find the value of 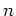 guaranteed by the error estimate to satisfy the same tolerance and see if the actual number of subintervals needed for simpson's rule to satisfy the tolerance is smaller.
guaranteed by the error estimate to satisfy the same tolerance and see if the actual number of subintervals needed for simpson's rule to satisfy the tolerance is smaller.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2007-02-19
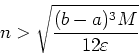
![]() is
is
![\begin{displaymath}n > \sqrt[4]{\frac{(b-a)^5 M}{180 \varepsilon}} \end{displaymath}](img27.png)