Suppose ![]() is a non-negative, continuous function defined on some
interval
is a non-negative, continuous function defined on some
interval ![]() . Then by the area under the curve
. Then by the area under the curve ![]() between
between
![]() and
and ![]() we mean the area of the region bounded above by the
graph of
we mean the area of the region bounded above by the
graph of ![]() , below by the
, below by the ![]() -axis, on the left by the vertical
line
-axis, on the left by the vertical
line ![]() , and on the right by the vertical line
, and on the right by the vertical line ![]() . All of the
numerical methods in this lab depend on subdividing the interval
. All of the
numerical methods in this lab depend on subdividing the interval
![]() into subintervals of uniform length.
into subintervals of uniform length.
In these simple rectangular approximation methods, the area above each subinterval is approximated by the area of a rectangle, with the height of the rectangle being chosen according to some rule. In particular, we will consider the left, right and midpoint rules.
The Maple student package has commands for visualizing these three rectangular area approximations. To use them, you first must load the package via the with command. Then try the three commands given below to help you understand the differences between the three different rectangular approximations. Note that the different rules choose rectangles which in each case will either underestimate or overestimate the area.
> with(student): > rightbox(x^2,x=0..4); > leftbox(x^2,x=0..4); > middlebox(x^2,x=0..4);There are also Maple commands leftsum, rightsum, and middlesum to sum the areas of the rectangles, see the examples below. Note the use of evalf to obtain the desired numerical answers.
> rightsum(x^2,x=0..4); > evalf(rightsum(x^2,x=0..4)); > evalf(leftsum(x^2,x=0..4)); > evalf(middlesum(x^2,x=0..4));
All of the Maple commands described so far in this lab can include a third
argument to specify the number of subintervals. The default is 4
subintervals. The example below approximates the area under ![]() from
from ![]() to
to ![]() using the rightsum command with 50,
100, 320 and 321 subintervals. As the number of subintervals
increases, the approximation gets closer and closer to the exact
answer. You can see this by assigning a label to the approximation,
assigning a label to the exact answer
using the rightsum command with 50,
100, 320 and 321 subintervals. As the number of subintervals
increases, the approximation gets closer and closer to the exact
answer. You can see this by assigning a label to the approximation,
assigning a label to the exact answer ![]() and taking their
difference. The closer you are to the actual answer, the smaller the
difference. The example below shows how we can use Maple to
approximate this area with an absolute error no greater than 0.1.
and taking their
difference. The closer you are to the actual answer, the smaller the
difference. The example below shows how we can use Maple to
approximate this area with an absolute error no greater than 0.1.
> exact := 4^3/3; > estimate := evalf(rightsum(x^2,x=0..4,50)); > evalf(abs(exact-estimate)); > estimate := evalf(rightsum(x^2,x=0..4,100)); > evalf(abs(exact-estimate)); > estimate := evalf(rightsum(x^2,x=0..4,320)); > evalf(abs(exact-estimate)); > estimate := evalf(rightsum(x^2,x=0..4,321)); > evalf(abs(exact-estimate));
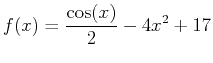 on the interval
on the interval
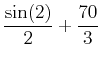 . Enter this value into Maple and label it exact. Look at the decimal version of the exact answer and compare it to the answers above. Then use the command rightbox to explain why the rightsum command yields a value that is always less than the exact value of the area. You may use a value of
. Enter this value into Maple and label it exact. Look at the decimal version of the exact answer and compare it to the answers above. Then use the command rightbox to explain why the rightsum command yields a value that is always less than the exact value of the area. You may use a value of
f:=x->sqrt(16-x^2); exact:=16*Pi/2;Use the area approximations leftsum and middlesum to determine the minimum number of rectangles required to estimate the area of the circle with error no greater than 0.1. Based on your results, which approximation method is better, left hand endpoint rule or the midpoint rule?