


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to study applications of
exponential and logarithmic functions. These are used to model many
types of growth and decay.
The simple model for growth is exponential growth, where
it is assumed that
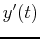 is proportional to
is proportional to 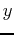 . That is,
. That is,
Separating the variables and integrating (see section 4.4 of the text),
we have
so that
In the case of exponential growth, we can drop the absolute value
signs around 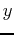 , because
, because 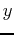 will always be a positive quantity.
Solving for
will always be a positive quantity.
Solving for 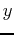 , we obtain
, we obtain
which we may write in the form 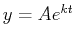 , where
, where 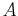 is an
arbitrary positive constant.
is an
arbitrary positive constant.
In a sample of a radioactive material, the
rate at which atoms decay is proportional to the amount of material present.
That is,
where 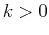 is a constant. This is the same equation as in exponential growth,
except that
is a constant. This is the same equation as in exponential growth,
except that 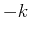 replaces
replaces 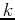 . The solution is
. The solution is
where 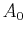 is a positive constant. Physically,
is a positive constant. Physically, 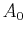 is the amount of
material present at
is the amount of
material present at 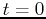 .
.
Radioactivity is often expressed in terms of an element's half-life.
For example, the half-life of carbon-14 is 5730 years. This statement means
that for any given sample of
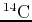 , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is 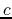 years, it must be
that
years, it must be
that
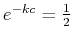 , so that
, so that 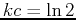 and
and
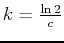 .
.
What is usually called Newton's law of cooling is a simple model for
the change in temperature of an object that is in contact with an
environment at a different temperature. It says that the rate of
change of the temperature of an object is proportional to the
difference between the object's temperature and the temperature of the
environment. Mathematically, this can be expressed as the differential
equation
where 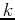 is the constant of proportionality and
is the constant of proportionality and
 is
the temperature of the environment. Using a technique called
separation of variables it isn't hard to derive the solution
is
the temperature of the environment. Using a technique called
separation of variables it isn't hard to derive the solution
where 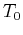 is the temperature of the object at
is the temperature of the object at 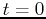 .
.
Information can be thought of as of a physical quantity which can be measured. According to the Gallup Institute, information news diffuses through a fixed adult population of size 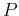 at a rate of time proportional to the number of people who have not heard the news.
at a rate of time proportional to the number of people who have not heard the news.
If 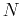 is the number of people who have heard the news after t days, then
is the number of people who have heard the news after t days, then
The initial condition 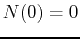 yields the solution
yields the solution
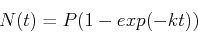
- Suppose that the population of a certain bacteria can be modeled by an exponential function. In a particular experiment, the number of bacteria was
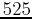 at
at 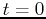 . Suppose the population doubles every six hours. Find the value of the growth constant
. Suppose the population doubles every six hours. Find the value of the growth constant 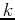 and use it to predict the number of bacteria that would have been present after a day and a half. Check your answer by repeated doubling of the initial number of bacteria.
and use it to predict the number of bacteria that would have been present after a day and a half. Check your answer by repeated doubling of the initial number of bacteria.
- Exponential growth can also be used to model the growth of investments. Suppose that the value
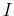 of an investment satisfies the differential equation
of an investment satisfies the differential equation
where 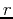 is the interest rate. If the interest rate is
is the interest rate. If the interest rate is 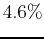 per year and you start with an investment of $8,500, what would the net gain be after 20 years? Approximately how many years would it take to save $50,000?
per year and you start with an investment of $8,500, what would the net gain be after 20 years? Approximately how many years would it take to save $50,000?
- The concentration of a medication in the bloodstream can be modeled as an exponential decay problem
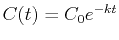 where the
where the 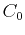 is the initial concentration,
is the initial concentration, 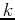 is the decay constant, and
is the decay constant, and 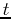 is time in hours. Suppose the initial dose is
is time in hours. Suppose the initial dose is 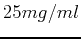 and after one hour, the medication is only 90% as effective. How many hours will it take for the drug to no longer be effective at 15% effectivenes?
and after one hour, the medication is only 90% as effective. How many hours will it take for the drug to no longer be effective at 15% effectivenes?
- Suppose that a coffee was served extra hot (
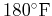 ) in a
) in a
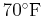 room and was
room and was
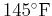 after 3 minutes. Approximately how many more minutes will it be too cold to drink (
after 3 minutes. Approximately how many more minutes will it be too cold to drink (
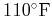 )?
)?
- Suppose that a group of 250 friends are on a social media website and 33% of them heard about a rumor 4 days after it happened. How many more days will it take for 90% of the people to have heard the rumor?



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2017-02-26
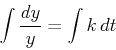
![]() , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is ![]() years, it must be
that
years, it must be
that
![]() , so that
, so that ![]() and
and
![]() .
.
![]() is the number of people who have heard the news after t days, then
is the number of people who have heard the news after t days, then
![]() yields the solution
yields the solution