


Next: About this document ...
Up: The Definite Integral -
Previous: Background
- 1.
- Consider the function f(x) = x3-6x2+5x+12 on the interval
[-1,3]. Use the command leftsum to
approximate the definite integral
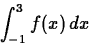
to two decimal places. Then explain why the leftsum and
rightsum commands give the same numerical values for the same
number of subintervals. (Hint - use the leftbox and
rightbox commands to see what is going on.)
- 2.
- Suppose that the velocity of a particle moving in one dimension
is given by
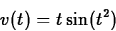
Find the average value of v(t) on the following time intervals.
- (a)
- [0,3]
- (b)
- [0,6]
- (c)
- [3,6]
- 3.
- Let the continuous function v(t) represent the velocity of a
particle moving
in one dimension. Let a and b be real numbers in the domain of v
and let c be (a+b)/2. That is, c is exactly halfway between a
and b. Show that the following equation is always satisfied
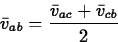
where 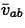 is the average value of v on the interval
[a,b],
is the average value of v on the interval
[a,b], 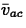 is the average value of v on the interval
[a,c], and
is the average value of v on the interval
[a,c], and 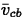 is the average value of v on the
interval [c.b]. Note - this is not a Maple problem. This problem is
a thinking problem. I would suggest leaving some space on your
worksheet and writing your answer in by hand. Part of using Maple is
learning when not to use it.
is the average value of v on the
interval [c.b]. Note - this is not a Maple problem. This problem is
a thinking problem. I would suggest leaving some space on your
worksheet and writing your answer in by hand. Part of using Maple is
learning when not to use it.



Next: About this document ...
Up: The Definite Integral -
Previous: Background
William W. Farr
1/16/1998
![]()
![]()
![]()
![]()
![]()
![]()