Subsections

• Rectangular approximations to definite integrals
• Computing definite integrals with Maple
• Definite integrals and average values

Background

Rectangular approximations to definite integrals

As we stated above, definite integrals are often used to find sums. As an example, suppose that v(t) represents the velocity of an object that moves in one dimension. At any instant of t, the value of v(t) can be positive, negative, or zero. If it is zero, the object is not moving at that instant. If it is not zero, then the sign of v(t) determines the direction of motion.

Now, suppose we were given a function v(t) for $0 \leq t \leq 4$,and we wanted to find the net distance traveled by the object over this time interval. If v(t) is constant, then this is easy to determine: distance is velocity times elapsed time. If the velocity is not constant, then it is more difficult to find the answer. The idea of using the integral is based on breaking the elapsed time up into subintervals. We approximate the distance traveled over each subinterval by picking an average velocity over that subinterval and using our formula distance equals velocity times elapsed time. Adding up the approximations for each subinterval gives an approximation to the net distance traveled. Intuitively, the more subintervals we use, the better the approximation will be. Note also that how we pick the average velocity over each subinterval can affect the accuracy of our approximation.

For example, suppose v(t)=3-t for $0 \leq t \leq 4$ and we want the approximate the net distance traveled. Suppose we use five subintervals and choose the velocity at the left endpoint of each subinterval for our average velocity. Then we can use the Maple leftsum command to calculate an approximate distance as shown below. A different approximation is obtained by using the velocity at the right endpoint of each subinterval, using the Maple rightsum command, and this is also shown below.

  > v := t -> 3-t;

  > plot(v(t),t=0..4);

  > evalf(leftsum(v(t),t=0..4,5));

  > evalf(rightsum(v(t),t=0..4,5));

Notice how different the two approximations are. However, if we increase the number of subintervals to 100, they are much closer.

  > evalf(leftsum(v(t),t=0..4,100));

  > evalf(rightsum(v(t),t=0..4,100));

These sums can also be interpreted geometrically, using the Maple leftbox and rightbox commands.

  > leftbox(v(t),t=0..4,5);

  > rightbox(v(t),t=0..4,5);

The sums we computed above with the leftbox and rightbox commands were obtained by adding up the areas of the rectangles with the following important convention: if a rectangle lies below the t axis, it appears in the sum with a minus sign. That is, we interpret a rectangle above the axis as having positive area and a rectangle below the axis as having negative area.

Computing definite integrals with Maple

In part 1 of this lab, we learned how to use the Maple int command to compute areas. The same command works to compute any definite integral, whether it corresponds to an area or not. For example, to compute the definite integral

$$\int_{-2}^{4} (2x-3)^5 \, dx$$

you could use the following Maple command.

  > int((2*x-3)^5,x=-2..4);

Sometimes you need to compute a definite integral involving a piecewise-defined function. For example, suppose you have a function f(x) defined as follows

$$f(x) = \left\{ \begin{array} {ll} 2-x^2 & \mbox{if $x < 1$} \\ x & \mbox{if $x \geq 1$} \end{array}\right.$$

and you needed to compute the definite integral

$$\int_{-5}^{5} f(x) \, dx$$

The best way to do this in Maple is to split it up into two integrals and use the appropriate formula, as shown below. How you split the integral up is determined by where the formula defining the function changes.

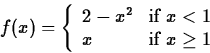
  > int(2-x^2,x=-5..1)+int(x,x=1..5);

Definite integrals and average values

If a function f is integrable over an interval [a,b], then we define the average value of f, which we'll denote as $\bar{f}_{ab}$,on this interval to be

$$\bar{f}_{ab} = \frac{1}{b-a} \int_{a}^{b} f(x) \, dx$$

Note that the average value is just a number. Note furthermore that we can rearrange the definition to give

$$\bar{f}_{ab} (b-a) = \int_{a}^{b} f(x) \, dx$$

If $f(x) \geq 0$ on [a,b], then the average value has the following geometrical interpretation: $\bar{f}_{ab}$ is the height of a rectangle of width b-a such that the area of this rectangle is equal to the area under the graph of f from a to b. The following example shows you how to compute an average. The last plot command shows the function and the top of this rectangle.

  > f :=x ->  x*sin(x) ;

  > plot(f(x),x=0..Pi);

  > f_ave := int(f(x),x=0..Pi)/Pi;

  > plot({f(x),f_ave},x=0..Pi);