Background

In this section, we first discuss the glass exercise from part 1 of this lab to try to clear up any confusion that may remain. Then we discuss two examples that further illustrate applications of solids of revolution.

In part 1 of this lab, one of the exercises referred to a design for a drinking glass. The idea was to come up with a function f(x) which could be revolved about the x axis over a suitable interval to produce the glass. Two students came up with the following function.

$$f(x) = \left\{ \begin{array} {ll} x^4+0.088 & \mbox{if $x <... ... \\ 0.088+\sin(x-3) & \mbox{if $x \gt 3$} \end{array}\right.$$

Which can be entered in Maple with the following command.

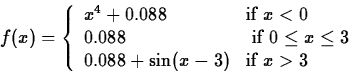
  > pz := x -> piecewise(x<0,x^4+0.088,x <=3,0.088,0.088+sin(x-3));

The final part of the exercise asked for the volume of the liquid-filled part of the glass. This would be

$$\pi \int_{3}^{4.5} f(x)^2 \, dx$$

The easiest way to compute this is with the following command.

  > evalf(Pi*int(pz(x)^2,x=3..4.5));

We now consider the following example. Suppose that a hole of radius 1 is to be bored through the center of a sphere of radius 2 and you are asked to compute the volume of the remaining part.

The hardest part of this example is setting it up as a solid of revolution problem. We know that we can generate a sphere of radius 2 by revolving the semi-circle $y=\sqrt{4-x^2}$ about the x axis. The sphere with a hole removed from the center can be obtained by revolving the region bounded by $y=\sqrt{4-x^2}$ and y=1. To see this, try the commands below.

  > g := x -> sqrt(4-x^2);

  > plot({g(x),1},x=-2..2);

To get the region right, we have to find the points where y=1 intersects the semi-circle. This is done below, and then the sphere with the hole is generated via revolve. You will probably have to move the plot around to see the hole.

  > solve(g(x)=1,x);

  > revolve({g(x),1},x=-sqrt(3)..sqrt(3));

The RevInt command can be used to set up the integral for the volume of the holed sphere in a simple way as follows.

  > RevInt({g(x),1},x=-sqrt(3)..sqrt(3));

The result of the RevInt command needs to be evaluated numerically as shown below.

  > evalf(RevInt({g(x),1},x=-sqrt(3)..sqrt(3)));

If you need an analytic answer, you are better off setting up the integral directly, as follows.

  > Pi*int(3-x^2,x=-sqrt(3)..sqrt(3));

The reason it is often better not to use RevInt is that it was designed primarily for demonstrations, and does not deal very intelligently with regions defined by two functions f and g.

As a third example, consider the following. A spherical tank of radius 25 meters is to be used to store liquid nitrogen. The tank has a sensor that reports the height of the liquid inside the tank. You have been asked to come up with a function that will convert the height of the liquid in the tank to the volume of the liquid in the tank.

We'll start by letting x be the height of the liquid in meters. Since this is a math class, it doesn't bother us at all that we'll be doing the problem with the tank on its side. First, we need a semi-circle of radius 25 and center x=25, y=0. That is we need to solve the equation

(x-25)²+y² = 25²

for y. If we do so, we get the equation

$$y = \sqrt{25^2-(x-25)^2}$$

Revolving this curve about the x axis for $0 \leq x \leq 50$ gives us our tank. Now suppose we want compute the volume of liquid when the tank is filled to a height x. (Recall that we've turned the tank on its side for our calculations.) This volume can be obtained by revolving our curve from 0 to x. That is, if we set up the curve defining the boundary of our tank as follows,

  > tank := x -> sqrt(625-(x-25)^2);

then the volume is given by the following function.

  > vol := x -> Pi*int(tank(t)^2,t=0..x);

which can be plotted to give the desired curve.