Exercises

1.

Consider the spherical tank example in the background section and answer the following questions.

(a)

Explain how the Maple commands for this exercise give the desired result. That is, take the Maple commands from the example and explain what they do as if you had done the problem on your own.

(b)

Explain why the curve giving volume as a function of height isn't a straight line.

2.

Suppose that a tank for holding molasses is to be constructed as a right circular cone of height 12 meters and base radius 3 meters. It is to be set up so that the point of the cone is at the bottom and the circular base is at the top. If x is the height of molasses in the cone, find and plot a function v(x) which gives the volume of molasses in the tank.

3.

A plastic bead is to be made by drilling a hole of radius a through the center of a sphere of radius r. (For this to make sense, note that we must have 0 < a < r.) To help you set this up, use the equation

$$y = \sqrt{r^2-x^2}$$

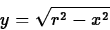
for the sphere and

y= a

to locate the hole. Find the volume of the bead in terms of the parameters r and a. (Hint - don't use the RevInt command. Set up the integrals directly.)