$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

Solids of Revolution

Introduction

The purpose of this lab is to use Maple to study solids of revolution. Solids of revolution are created by rotating curves in the x-y plane about an axis, generating a three dimensional object.

So far we have used the integral mainly to to compute areas of plane regions. It turns out that the definite integral can also be used to calculate the volumes of certain types of three-dimensional solids. The class of solids we will consider in this lab are called Solids of Revolution because they can be obtained by revolving a plane region about an axis.

As a simple example, consider the graph of the function for $-2\leq x \leq 2$ , which appears in Figure 1.

**Figure 1:** Plot of .

If we take the region between the graph and the x-axis and revolve it about the x-axis, we obtain the solid pictured in Figure 2.

To help you in plotting surfaces of revolution, A Maple procedure called revolve has been written. The command used to produce the graphs in Figures 1 and 2 is shown below. The revolve procedure, as well as the RevInt, LeftInt, and LeftDisk procedures described below are all part of the CalcP package, which must be loaded first. The last line in the example below shows the optional argument for revolving the graph of about the line instead of the default .

  > 
with(CalcP):

  > 
f := x -> x^2+1;

$\begin{maplelatex} \begin{displaymath} {f} := {x} \rightarrow {x}^{2} + 1 \end{displaymath}\end{maplelatex}$

  > 
plot(f(x),x=-2..2);

  > 
revolve(f(x),x=-2..2);

  > 
revolve(f(x),x=-2..2,y=-2)

**Figure 2:** Solid generated by rotating about the x-axis.

The revolve command has other options that you should read about in the help screen. For example, you can speed the command up by only plotting the surface generated by revolving the curve with the nocap argument, and you can also plot a solid of revolution formed by revolving the area between two functions. Try the following examples. (Note: The last example shows how to use revolve with a function defined piecewise using the piecewise command.)

  > 
revolve(f(x),0.5,x=-2..2,y=-1);

  > 
 revolve(cos(x),x=0..4*Pi,y=-2,nocap);

  > 
revolve(5,x^2+1,x=-2..2);

  > 
g := x -> piecewise(x<0,-x+1/2,x^2-x+1/2);

$\begin{maplelatex} \begin{displaymath} g := x\rightarrow \mathrm{piecewise}(x < ... ... \,x^{2} - x + {\displaystyle \frac {1}{2}} ) \end{displaymath}\end{maplelatex}$

  > 
revolve(g(x),x=-1..2);

It turns out that the volume of the solid obtained by revolving the region in Figure 1 between the graph and the -axis about the -axis can be determined from the integral

$\begin{displaymath}\pi \int_{-2}^2 (x^2+1)^2 \, dx\end{displaymath}$

to have the value $\frac{412}{15} \pi$ . More generally, if you revolve the area under the graph of

for $a \leq x \leq b$ about the x-axis, the volume is given by

$\begin{displaymath}\pi \int_{a}^{b} (g(x))^2 \, dx.\end{displaymath}$

Where does this formula come from? To help you understand it, Two more Maple procedures, RevInt and LeftDisk, have been written. The procedure RevInt sets up the integral for the volume of a solid of revolution, as shown below. The Maple commands evalf and value can be used to obtain a numerical or analytical value.

  > 
RevInt(f(x),x=-2..2);

$\begin{maplelatex} \begin{displaymath} { \pi}\,{\displaystyle \int_{-2}^{2}} (\,{x}^{2} + 1\,)^{2}\,{d}{ x} \end{displaymath}\end{maplelatex}$

  > 
value(RevInt(f(x),x=-2..2));

$\begin{maplelatex} \begin{displaymath} {\displaystyle \frac {412}{15}}\,{ \pi} \end{displaymath}\end{maplelatex}$

  > 
 evalf(RevInt(f(x),x=-2..2));

$\begin{maplelatex} \begin{displaymath} 86.28907824 \end{displaymath}\end{maplelatex}$

The integral formula given above for the volume of a solid of revolution comes, as usual, from a limit process. Recall the rectangular approximations we used for plane regions. If you think of taking one of the rectangles and revolving it about the x-axis, you get a disk whose radius is the height of the rectangle and thickness is $\Delta x$ , the width of the rectangle. The volume of this disk is $\pi h^2 \Delta x$ . If you revolve all of the rectangles in the rectangular approximation about the x-axis, you get a solid made up of disks that approximates the volume of the solid of revolution obtained by revolving the plane region about the x-axis.

To help you visualize this approximation of the volume by disks, the LeftDisk procedure has been written. The syntax for this procedure is similar to that for revolve, except that the number of subintervals must be specified. The examples below produce approximations with five and ten disks. The latter approximation is shown in Figure 3.

  > 
LeftDisk(f(x),x=-2..2,5);

  > 
LeftDisk(f(x),x=-2..2,10);

  > 
LeftInt(f(x),x=-2..2,5);

$\begin{maplelatex} \begin{displaymath} 99.52163404 \end{displaymath}\end{maplelatex}$

  > 
LeftInt(f(x),x=-2..2,10);

$\begin{maplelatex} \begin{displaymath} 89.62938708 \end{displaymath}\end{maplelatex}$

The two LeftInt commands above add up the volumes in the disk approximations of the solid of revolution.

**Figure 3:** Cylindrical approximation with to the solid generated by rotating about the x-axis.

Finding Volumes of Revolution

Since this involves straightforward integration, one may simply issue commands such as:

  > 
f:= x-> sqrt(x) +1;

$\begin{maplelatex} \begin{displaymath} f := x \rightarrow \sqrt(x) + 1 \end{displaymath}\end{maplelatex}$

  > 
vol:= int(Pi*f(x)^2, x=0..9);

$\begin{maplelatex} \begin{displaymath} vol := \frac{171}{2}\;\pi \end{displaymath}\end{maplelatex}$

  > 
evalf(vol);

$\begin{maplelatex} \begin{displaymath} 268.6061719 \end{displaymath}\end{maplelatex}$

Exercises

Compute the volume of the solid generated by revolving the region bounded by the axis and the graph of the function

$\begin{displaymath}h(x) = \displaystyle{\frac{1}{4}} + \displaystyle{\frac{2}{x+1}} - \cos(2x)exp(-x/4) \end{displaymath}$

for $0 \leq x \leq 6$ . Include a plot of the solid.
A maker of brass candlesticks plans to make a candlestick whose shape is given by revolving the function

$\begin{displaymath}f(x) = \displaystyle{ \frac{3}{x^2}} + \displaystyle{\frac{2}{5-x}} + \sin(\pi x) \end{displaymath}$

about the axis over the interval .
1. Use the revolve command to obtain a plot of the proposed candlestick.
2. Find the volume of the candlestick.
The candlesticks from the previous exercise are to be machined from a cast, dumbbell-shaped blank that consists of two cylinders connected by a smaller-diameter cylinder. (A blank is just the name used in fabrication for the piece used as a starting point for the machining process.) The shape of the blank is given by revolving the function

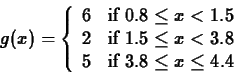
$\begin{displaymath}g(x) = \left\{ \begin{array}{ll} 6 & \mbox{if $0.8 \leq x < ... ...\ 5 & \mbox{if $3.8 \leq x \leq 4.4$}\\ \end{array}\right. \end{displaymath}$

about the axis over the interval . Here is a Maple command you can use to define .
```
  > 
g := x -> piecewise(x<1.5,6,x<3.8,2,5);
```
1. Use the revolve command to obtain a plot of the blank.
2. Compute the volume of the blank.
3. When the blank is machined into a candlestick, material is removed from the blank. Find the volume of material that must be removed.

$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

Jane E Bouchard
2001-04-03

Solids of Revolution

Introduction

Background

Finding Volumes of Revolution

Exercises