


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
One use for the definite integral is to find area. There are some things to remember. One is that definite integrals can be negative but area cannot. So remeber that area is calculated as the integral of the top function minus the bottom (even if that top function is the x-axis)
> plot(x^2-4,x=-3..3);
If you wanted to find the area created by the parabola and the x-axis you need to use the fact that the equation of the x axis is 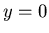 . Integrate the top function from the bottom with the limits of integration being the intersection points.
. Integrate the top function from the bottom with the limits of integration being the intersection points.
>int(0-x^2-4,x=-2..2);
The next example shows how Maple can be used to find the intersection points and then use these to calculate the bounded area.
> f := x-> -x^2+4*x+6;
> g := x-> x/3+2;
> plot({f(x),g(x)},x=-2..6);
> a := fsolve(f(x)=g(x),x=-2..0);
> b := fsolve(f(x)=g(x),x=4..6);
> int(f(x)-g(x),x=a..b);
This final example shows how to break up the area if necessary. If you want to find the area bounded by the three graphs:
> f:=x->x+4;g:=x->-x+5;h:=x->sqrt(x^2+3);
> plot({f(x),g(x),h(x)},x=-4..4,color=red);
Notice that there are two functions that bound the top of the area. To find the complete area , break the problem into two. First find the area of 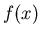 and the square root and then find the area of
and the square root and then find the area of 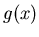 and the square root. Then add these results. As usual you need to find the intersection points.
and the square root. Then add these results. As usual you need to find the intersection points.
> solve(f(x)=g(x),x);
> solve(f(x)=h(x),x);
> solve(g(x)=h(x),x);
Now do the two integrals and add them.
>evalf(int(f(x)-h(x),x=-13/8..1/2)+int(g(x)-h(x),x=1/2..11/5));
- Find the area bounded by the two functions
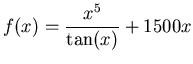 and
and
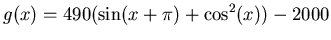 . First plot the two functions over the domain
. First plot the two functions over the domain
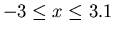 .
.
- Find the area bounded by the three functions
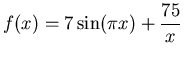 ,
,
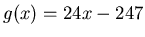 and
and
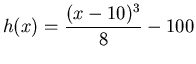 . First create a plot that clearly shows the bounded area.
. First create a plot that clearly shows the bounded area.
- Find the total area bounded by the functions
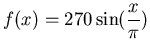 and
and
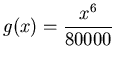 . (Hint: there is more than one bounded region).
. (Hint: there is more than one bounded region).



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2006-03-23
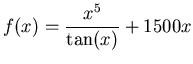 and
and
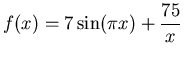 ,
,
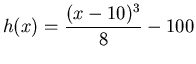 . First create a plot that clearly shows the bounded area.
. First create a plot that clearly shows the bounded area.
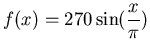 and
and
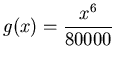 . (Hint: there is more than one bounded region).
. (Hint: there is more than one bounded region).
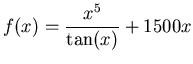 and
and
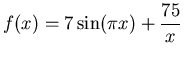 ,
,
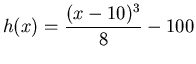 . First create a plot that clearly shows the bounded area.
. First create a plot that clearly shows the bounded area.
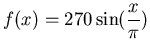 and
and
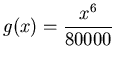 . (Hint: there is more than one bounded region).
. (Hint: there is more than one bounded region).