Subsections

• Purpose
• Background
• A. Probability Distribution
• B. Some Particular Probabilities
• C. Application to Manufacturing
• Historical Remarks

Improper Integrals Part 2

Purpose

This lab is a continuation of the first lab. It's purpose is to apply the mathematical results obtained by you there to quality control in mass production. We will see how the ability to work with integrals such as those from the firstlab can be applied to improper integrals.

Background

In the first lab, you showed that the integral

$$\int_{-\infty}^{\infty} e^{\frac{-(x-x_0)^2}{2\sigma^2}} dx =\sigma \sqrt{2 \pi}$$

which is equivalent to

$$\frac{1}{\sigma \sqrt{(2 \pi)}} \int_{- \infty}^{\infty} e^{\frac{(-(x-x_0)^2)}{2 \sigma^2}} dx = 1$$

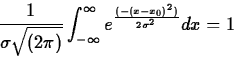
You may have gotten 1.772 in lab 1, which is $\sqrt{\pi}$.

You also explored the effects of the parameters x₀ and $\sigma$; the former is the center of the bell shaped curve and the latter effects how spread out the curve is. Together, they cause the points of inflection to be at $x_0 \pm \sigma .$ The mean of the curve is denoted by x₀ and $\sigma$ is called the standard deviation.

A. Probability Distribution

Consider the function

$$F(x_1,x_2) = \frac{1}{\sigma \sqrt{(2\pi)}} \int_{x_1}^{x_2}e^{\frac {-(x-x_0)^2}{2 \sigma ^2}} dx$$

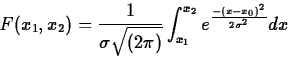
This is called the general normal distribution.
This has the interpretation of the fraction of the population being described which is between x₁ and x₂. Note that if we let x₁ go to $- \infty$ and x₂ go to $\infty$, we get the integral whose value we know to be one. That it is one indicates that the entire population is accounted for. Using properties of integrals, we may easily establish some other facts:

$$F(0, \infty) = 0.5$$

$$F(- \infty, 0) = 0.5$$

F(-a , a ) = 2 F(0,a)

$$F(a, \infty) = 0.5 - F(0,a)$$

Please establish all four of these in your report. For purposes of comparison, we will call the case where x₀ = 0 and $\sigma$ the standard normal distribution.

B. Some Particular Probabilities

Referring to the standard normal distribution, please compute, to 4 decimal places, by numerical methods such as those employed in part #1, the following:

1.

F(0,1)

2.

F(0,2)

3.

F(0,3)

Now the general normal distribution is related to the standard normal distribution by the variable change

$$u= \frac{(x-x_0)}{\sigma}=1$$

Taking this into account, argue on algebraic grounds why

4.

2F(0,1) = the fraction of the population 1 standard deviation from the mean.

5.

2F(0,2) = the fraction of the population 2 standard deviations from the mean

6.

2F(0,3) = the fraction of the population 3 standard deviations from the mean

7.

Show in general, 2F(0,u) = the fraction of the population u standard deviations from the mean

As an example, if the mean of a population is 400 and the standard deviation is 100, what fraction of the population is between

8.

300 and 500

9.

400 and 600

10.

greater than 500 ?

C. Application to Manufacturing

Here, we assume we have been contracted by a company which supplies pistons to major auto manufacturers. Our company will be making 2,000,000 of the same piston for a production run of 500,000 cars by the auto manufacturer. The design specification for the diameter of the pistons states that they must be 2.700" $\pm 0.003$. In other words, the ideal piston is 2.700 inches, but anything from 2.697 to 2.703 inches is acceptable. However, if the piston is bigger than 2.703, it may sieze in the motor when used, and if it is smaller than 2.697, it will wear excessively and allow unacceptable oil consumption. In either case, the automanufacturer might have to rebuild the motor under warranty, with the average cost being $500. After collecting some data, we find that the standard deviation, $\sigma$, for this population is 0.002.

1.

What fraction of the population is defective? What is the likely cost associated with this level?

2.

In manufacturing, the term defect rate is sometimes used. It means the number of items for every million produced which are defective.

i.

What is the current defect rate? (the units would be defects per million, or dpm)

ii.

Suppose we wished to have a defect rate of 50,000 dpm. What would $\sigma$ have to be reduced to in order for this to occur?

3.

Suppose it cost $20,000,000 in training and new (more accurate) equipment to reduce $\sigma$ to .001. Would it be worth it? Why or why not?

4.

In the early 1990s, Motorola began a program called "Six Sigma" which, mathematically, meant that $\pm 6$ units of standard deviation would be within design specifications. What would the defect rate be in such a case?

Historical Remarks

The mathematical methods and approaches described in Part Three are at the basis of Statistical Quality Control. SQC and the management techniques associated with it were developed in the United States in the 1930s. After World War II, they were brought to Japan by the noted statistician William Edwards Deming (1901-1993) were they were incorporated into the auto industry there and played a prominent role in rise of that industry. A non technical history of the auto industry which describes Deming and his role may be found in The Reckoning by David Halberstam.