


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to introduce you to the notion
of improper integral and to give you practice with this concept by
using it to prove convergence or divergence of integrals involving
unbounded integrands or unbounded intervals or both.
Our basic theorem for
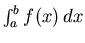 is that the integral
exists if
is that the integral
exists if 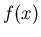 is continuous on the closed interval
is continuous on the closed interval ![$[a,b]$](img3.png) . We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on
. We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on ![$[a,b]$](img3.png) .
However, we don't have any theory to help us deal with integrals
.
However, we don't have any theory to help us deal with integrals
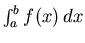 involving one or more of the following.
involving one or more of the following.
- Functions
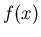 , for example rational functions, that have
vertical asymptotes in
, for example rational functions, that have
vertical asymptotes in ![$[a,b]$](img3.png) (or are not bounded on
(or are not bounded on ![$[a,b]$](img3.png) ).
).
- Integrals where the interval
![$[a,b]$](img3.png) is unbounded, for example
intervals like
is unbounded, for example
intervals like 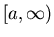 ,
, ![$(-\infty, b]$](img5.png) , or
, or
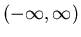 .
.
We have already seen at least one example of the problems you can run
into if the function is unbounded. Recall the clearly absurd result
that is obtained by blindly applying the FTOC. The second type of
problem, where the interval of integration is unbounded, occurs often
in applications of calculus, such as the Laplace and Fourier
transforms used to solve differential equations. It also occurs in
testing certain kinds of infinite series for convergence or
divergence, as we will learn later.
We start with the following definition.
Definition 1
We say that the integral
is improper if
one or both of the following conditions is satisfied.
- The interval of integration is unbounded.
- The function
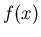 has an infinite discontinuity at some point
has an infinite discontinuity at some point
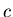 in
in ![$[a,b]$](img3.png) . That is,
. That is,
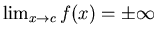 .
.
To see how to handle the problem of an unbounded integrand, we start
with the following special cases.
Definition 2
Suppose that
is continuous on
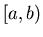
, but
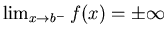
. Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
Definition 3
Suppose that
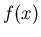
is continuous on
![$(a,b]$](img14.png)
, but
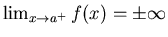
. Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
Cases where 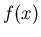 has an infinite discontinuity only at an interior
point
has an infinite discontinuity only at an interior
point 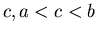 are handled by writing
are handled by writing
and using the definitions to see if the integrals on the right-hand
side exist. If both exist then the integral on the left-hand
side exists. If either of the integrals on the right-hand side
diverges, then
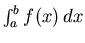 does not exist.
does not exist.
Here is a simple example using Maple to show that
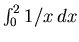 doesn't exist.
doesn't exist.
> ex1 := int(1/x,x=a..2);
> limit(ex1,a=0,right);
The example above used the right option to limit
because the right-hand limit was needed. If you need a left-hand
limit, use the left option in the limit command. Maple can usually do the limit within the int command.
> int(1/x,x=0..2);
These are handled in a similar fashion by using limits. The definition
we need the most is given below.
Definition 4
Suppose
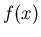
is continuous on the unbounded interval
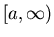
.
Then we define
provided the limit on the right-hand side exists and is finite, in
which case we say the integral converges and and is equal to the value
of the limit. If the limit is infinite or fails to exist we say the
integral diverges or fails to exist.
The other two cases are handled similarly. You are asked to provide
suitable definitions for them in one of the exercises.
Using the definition for
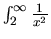 .
.
> ex2:=int(1/x^2,x=2..a);
> limit(ex2,a=infinity);
This command shows that Maple takes the limit definition into account in the int command.
> int(1/x^2,x=2..infinity);
- Determine if the following improper integrals exist. If they do
exist, report their values. If they do not exist, show why not.
-
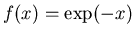 , interval
, interval 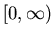 .
.
-
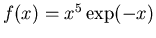 , interval
, interval 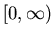 .
.
-
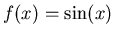 , interval
, interval 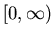 .
.
-
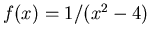 , interval
, interval ![$[-2, 2]$](img27.png) .
.
- Recall from Calculus II how to compute the volume of a solid of revolution.
- Find the volume of the solid obtained by revolving the curve
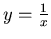 about the x-axis, between
about the x-axis, between 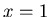 and
and 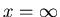 .
.
- Then find the volume of the solid by revolving the curve
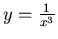 about the x-axis, between
about the x-axis, between 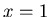 and
and 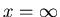 .
.
- Plot both functions.
- Find the surface area of each solid of revolution. The formula for the surface area is given on page 298 of the text.
- Is it possible to have a finite volume but an infinite surface area?



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2004-08-26
![]() is that the integral
exists if
is that the integral
exists if ![]() is continuous on the closed interval
is continuous on the closed interval ![]() . We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on
. We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on ![]() .
However, we don't have any theory to help us deal with integrals
.
However, we don't have any theory to help us deal with integrals
![]() involving one or more of the following.
involving one or more of the following.
![]() has an infinite discontinuity only at an interior
point
has an infinite discontinuity only at an interior
point ![]() are handled by writing
are handled by writing