


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to introduce you to curve computations
using Maple for parametric curves and vector-valued functions in the
plane.
The easiest way to define a vector function or a parametric curve is to use the Maple list notaion with square brackets[]. Strictly speaking, this does not define something that Maple recognizes as a vector, but it will work with all of the commands you need for this lab.
To assist you, there is a worksheet associated with this lab that
contains examples similar to some of the exercises.On your Maple screen go to File - Open then type the following in the white rectangle:
\\storage\academics\math\calclab\MA1023\Vector_start_A14.mw
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read through the exercises, start up Maple, load the worksheet, and go through it carefully. Then you can start working on the exercises.
>r:=t->[3*sin(t),3*cos(t)];
You can evaluate this function at any value of t in the usual way.
>r(0);
This is how to access a single component.
>r(t)[1];
>r(t)[2];
The VPlot command is in the CalcP package so you have to load it first. If you get an error from this command, ask for help right away. A few examples are shown below.
>with(CalcP7):
>VPlot([t^2,t^3-t],t=-1.5..1.5);
>VPlot(r(t),t=0..2*Pi);
The graph of a parametric curve may not have a slope at every point on
the curve. When the slope exists, it is given by the formula:
In Maple, the slope of a parametric curve can be calculated using the 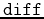 command as in the example below.
command as in the example below.
> r := -> [3*sin(t),3*cos(t)];
> slope := diff(r(t)[2],t)/diff(r(t)[1],t);
The vector equation for the line passing through the point
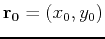 parallel to the vector
parallel to the vector
![$\mathbf{v}=[v_1,v_2]$](img4.png) is given by:
is given by:
Below is an example in Maple using this parametric form of a line that is tangent to the curve 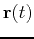 defined above at
defined above at
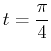 . The plot of the curve and the line on the same graph verifies that the line is tangent at the given point.
. The plot of the curve and the line on the same graph verifies that the line is tangent at the given point.
>eval(slope,t=Pi/4);
Since the slope at
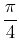 is -1, we want the line through the point
is -1, we want the line through the point
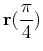 , parallel to the vector
, parallel to the vector ![$[1,-1]$](img10.png) .
.
>line:=t->r(Pi/4)+[t,-t];
>with(plots):
>a:=VPlot(r(t),t=-Pi..Pi):
>b:=VPlot(line(t),t=-Pi..Pi):
>display(a,b);
Parametric curves often represent the motion of a
particle or mechanical system. When we think of a parametric curve as representing motion, we need a way to measure the distance traveled by the particle. This distance is given by the arc length, 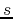 , of a curve. For a parametric curve
, of a curve. For a parametric curve
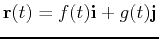 , the arc length of the curve for
, the arc length of the curve for
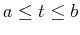 is given
below.
is given
below.
While the concept of arc length is very useful for the theory of
parametric curves, it turns out to be very difficult to compute in all
but the simplest cases. The maple command below shows that the arclength of a circle with the parametrization
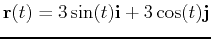 has constant arclength.
has constant arclength.
> evalf(int(sqrt(diff(3*sin(t),t)^2+diff(3*cos(t),t)^2),t=0..2*Pi));
For this lab, we will also assume that we have a vector-valued function 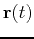 that gives the position at time
that gives the position at time 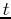 of a moving point
of a moving point 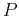 in the plane. The velocity of this point is given by the derivative
in the plane. The velocity of this point is given by the derivative 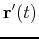 and the acceleration is given by the second derivative,
and the acceleration is given by the second derivative, 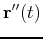 . In many applications of curvilinear motion, we need to know the magnitude of the velocity, or the speed. This is easy to compute - just take the magnitude
. In many applications of curvilinear motion, we need to know the magnitude of the velocity, or the speed. This is easy to compute - just take the magnitude 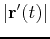 . If you think of the speed as the rate of change of distance along the curve, and recall that arc length is distance measured along the curve, then you have the following interpretation of the speed
. If you think of the speed as the rate of change of distance along the curve, and recall that arc length is distance measured along the curve, then you have the following interpretation of the speed
where 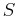 is arc length.
If the speed is not zero for any value of
is arc length.
If the speed is not zero for any value of 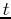 in the interval
in the interval 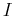 , then it is possible to define a unit vector,
, then it is possible to define a unit vector, 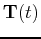 that is tangent to the curve as follows.
that is tangent to the curve as follows.
Using this definition, you can write the velocity in the following form.
This is not the most useful form for calculating the velocity, but it does lead to a useful way of thinking about the acceleration experience by a particle moving in a curvilinear path. If the path is a straight line, acceleration depends only on whether the particle is speeding up or slowing down. In a curve, however, there is an additional acceleration, called the centripetal acceleration, that is needed to keep the particle moving on the curve. The magnitude of this acceleration depends on the speed of the car and how much the path is curving. It turns out that you can quantify this with an intrinsic property of the curve called the curvature, usually denoted 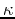 , defined by the following equation.
, defined by the following equation.
That is, the curvature is the magnitude of the rate of change of the tangent vector 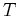 with respect to arc length. For example, the curvature of a straight line is zero and it can be shown that the curvature of a circle of radius
with respect to arc length. For example, the curvature of a straight line is zero and it can be shown that the curvature of a circle of radius 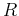 is the same for every point on the circle and is given by
is the same for every point on the circle and is given by 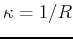 . The Maple Speed command computes the speed of a vector function and the Curvature command computes the curvature of a vector function. The syntax for these commands is shown in the example below that computes the speed of a particle traveling along the path traced by the curve
. The Maple Speed command computes the speed of a vector function and the Curvature command computes the curvature of a vector function. The syntax for these commands is shown in the example below that computes the speed of a particle traveling along the path traced by the curve
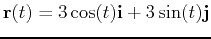 at
at 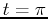 , the curvature of the curve at
, the curvature of the curve at 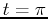 and the arclength of the curve over the interval
and the arclength of the curve over the interval
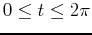 .
.
> r:=t->[3cos(t),3sin(t)];
> v:=diff(r(t),t);
> sqrt(v[1]^2+v[2]^2);
> Speed(r(t),t);
> Speed(r(t),t=Pi);
> Curvature(r(t),t=Pi);
> int(sqrt(v[1]^2+v[2]^2),t=0..2*Pi);
- Consider the vector function
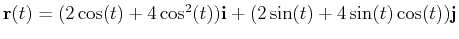 for
for
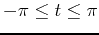 .
.
- Calculate the
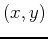 coordinate point on the curve at
coordinate point on the curve at
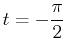 and the slope of the curve at
and the slope of the curve at
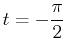 .
.
- Define the vector equation of the line through the point above tangent to the curve at that point.
- Plot the graph of
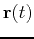 and this tangent line on the same graphover the interval
and this tangent line on the same graphover the interval
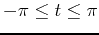 .
.
- Given the vector function
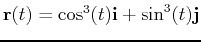
- Plot the vector function over the interval
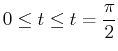 .
.
- Calculate the speed of the particle at
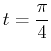 using the magnitude of the velocity and verify using Maple's Speed command. Calculate the curvature at
using the magnitude of the velocity and verify using Maple's Speed command. Calculate the curvature at
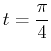 using Maple's Curvature command.
using Maple's Curvature command.
- Calculate the arclength
 over the interval
over the interval
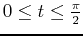 .
.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2014-09-22
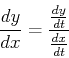
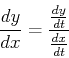
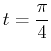 . The plot of the curve and the line on the same graph verifies that the line is tangent at the given point.
. The plot of the curve and the line on the same graph verifies that the line is tangent at the given point.
![]() that gives the position at time
that gives the position at time ![]() of a moving point
of a moving point ![]() in the plane. The velocity of this point is given by the derivative
in the plane. The velocity of this point is given by the derivative ![]() and the acceleration is given by the second derivative,
and the acceleration is given by the second derivative, ![]() . In many applications of curvilinear motion, we need to know the magnitude of the velocity, or the speed. This is easy to compute - just take the magnitude
. In many applications of curvilinear motion, we need to know the magnitude of the velocity, or the speed. This is easy to compute - just take the magnitude ![]() . If you think of the speed as the rate of change of distance along the curve, and recall that arc length is distance measured along the curve, then you have the following interpretation of the speed
. If you think of the speed as the rate of change of distance along the curve, and recall that arc length is distance measured along the curve, then you have the following interpretation of the speed
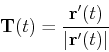
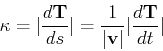
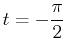 and the slope of the curve at
and the slope of the curve at
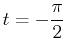 .
.
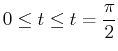 .
.
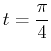 using the magnitude of the velocity and verify using Maple's Speed command. Calculate the curvature at
using the magnitude of the velocity and verify using Maple's Speed command. Calculate the curvature at
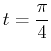 using Maple's Curvature command.
using Maple's Curvature command.