


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to introduce you to the concept of radius of convergence of
power series and Taylor series.
To assist you, there is a worksheet associated with this lab that
contains examples similar to some of the exercises. You can access this worksheet by typing in the search field (mag
nifying glass next to start menu):
\\storage.wpi.edu\academics\math\calclab\MA1023\Powseries_start_A19.mw
The general form of the Taylor polynomial approximation of order 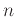 to
to 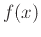 is given by the following
is given by the following
Theorem 1
Suppose that 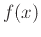 is a smooth function in some open interval
containing
is a smooth function in some open interval
containing 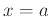 . Then the
. Then the 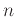 th degree Taylor polynomial of the
function
th degree Taylor polynomial of the
function 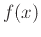 at the point
at the point 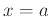 is given by
which can be written more compactly with summation notation.
is given by
which can be written more compactly with summation notation.
The notation
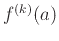 is used in the definition to stand for the value of the
is used in the definition to stand for the value of the
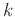 -th derivative of
-th derivative of 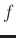 at
at 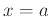 . That is,
. That is,
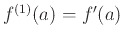 ,
,
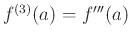 , and so on. By convention,
, and so on. By convention,
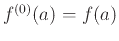 . Note that
. Note that 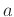 is fixed and so the derivatives
is fixed and so the derivatives 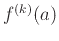 are
just numbers. That is, a Taylor polynomial has the form
are
just numbers. That is, a Taylor polynomial has the form
which you should recognize as a power series that has been truncated.
The Ratio Test for convergence of a series can be thought of as a measurement of how fast the series is increasing or decreasing. This can be found by looking at the ratio
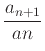 as
as
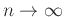 .
.
Given the series
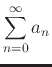 , suppose that
, suppose that
Then
- the series converges if
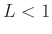 ,
,
- the series diverges if
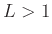 ,
,
- the test is inconclusive if
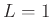 .
.
The radius of convergence of a series can usually be found by using the ratio test:
Next, you would need to solve for the interval of 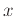 values such that
values such that 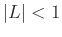 . This, however, does not account for convergence or divergence at the endpoints of the interval. Those would need to be tested individually.
. This, however, does not account for convergence or divergence at the endpoints of the interval. Those would need to be tested individually.
The general term 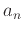 for a series
for a series
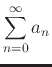 can be defined in Maple as a function of
can be defined in Maple as a function of 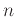 and the ratio test can be performed as follows:
and the ratio test can be performed as follows:
> a := n-> (1/2)^n
> limit(a(n+1)/a(n),n=infinity)
The same commands can be used to determine the radius of convergence of a power series where you would then need to solve for the values of x that would make the absolute value of the limit less than 1.
> a := n-> x^n
> L:= limit(a(n+1)/a(n),n=infinity)
> solve(abs(L)<1,x)
This approach can also be used to determine the interval that a Taylor series converges to the function that it is approximating. However, you must first identify the general term of the series as shown below.
> f := x-> cos(x)
> taylor(f(x),x=0,10)
> a:= n-> (-1)^n(2x)^n/(2n)!
> seq(a(n),n=0..5)
> L:= simplify(limit(a(n+1)/a(n),n=infinity))
> solve(abs(L)<1,x)
- Use the ratio test to determine if each of the given series converges or diverges.
- a)
-
- b)
-
- c)
-
- Use the ratio test to find the interval of convergence for each of the following series. When necessary, be sure to explain whether or not to include the endpoints of the interval.
- a)
-
- b)
-
- Find the Taylor/power series for each function listed below about
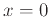 . Write the general term of the series and define it as
. Write the general term of the series and define it as 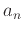 in Maple (Use the seq command to check that the terms match the terms of the series. Then, use the ratio test to determine the interval of
in Maple (Use the seq command to check that the terms match the terms of the series. Then, use the ratio test to determine the interval of 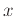 values over which the Taylor series converges to the given function.
values over which the Taylor series converges to the given function.
-
-
-
-
- Recall the function,
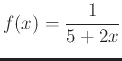 , from last week's lab. Use the procedure from the last exercise to verify your interval of convergence.
, from last week's lab. Use the procedure from the last exercise to verify your interval of convergence.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2019-09-27
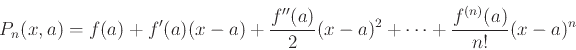
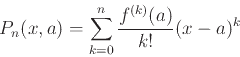
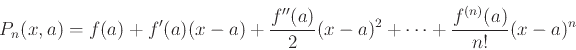
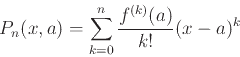
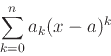
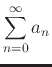 , suppose that
, suppose that
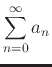 can be defined in Maple as a function of
can be defined in Maple as a function of 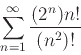
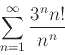
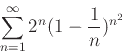
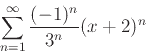
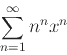
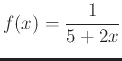 , from last week's lab. Use the procedure from the last exercise to verify your interval of convergence.
, from last week's lab. Use the procedure from the last exercise to verify your interval of convergence.