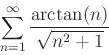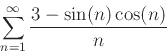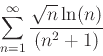Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to learn how to define sequences and series using Maple as well as observe their plots and test for convergence.
To assist you, there is a worksheet associated with this lab that you can copy into your home directory by going to your computer's start menu and choose run. In the search field (magnifying glass next to start menu) type:
\\storage.wpi.edu\academics\math\calclab\MA1023\Seq_Series_start_A19.mw
A sequence is an infinite list of numbers with a specific pattern. An infinite series is the sum of an infinite sequence. More precisely, the sum of an infinite series is defined as the limit of the sequence of the partial sums of the terms of the series, provided this limit exists. If no finite limit exists, then we say that the series is divergent.
The sum of an infinite series is defined as
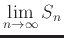 , where
, where 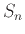 is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing
is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing 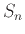 as a function of n, it is usually not possible to find sums by directly using the definition.
as a function of n, it is usually not possible to find sums by directly using the definition.
So, if we can generally not work from the definition, what can be done? There are several convergence tests that provide us with some needed tools. These are tests that tell us if a series converges, but in the case that the series does converge, does not tell us the sum of the series. One of the convergence tests that will be used in this lab is the integral test.
The Integral Test for convergence is a method used to test convergence of an infinite series of nonnegative terms.
The series
converges if and only if the integral
is finite, where 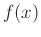 is a positive, non-increasing and continuous function defined on the interval
is a positive, non-increasing and continuous function defined on the interval 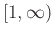 and
and 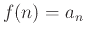 an for all
an for all 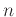 .
.
Consider the series
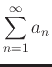 and
and
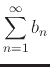 .
.
- If
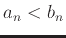 for
for 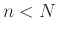 , where
, where 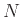 is some integer and
is some integer and
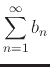 converges, then
converges, then
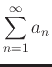 converges also.
converges also.
- If
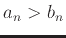 for
for 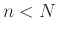 , where
, where 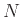 is some integer and
is some integer and
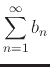 diverges, then
diverges, then
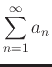 diverges also.
diverges also.
- Define the sequence
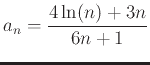 in Maple as a function of
in Maple as a function of 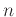 ,
,
- a
- List the first twenty terms and plot the first fifty terms of the sequence. Determine if the sequence appears to converge or diverge? If it seems to converge, to what does it converge?
- b
- Define a function for the sum of the sequence. List the first twenty terms and plot the at least the first fifty terms of the sequence of partial sums. Determine if the series converges or diverges? If it seems to converge, to what does it converge?
- c
- Calculate a limit of the sequence and a limit of the series to check your answers.
- For each sereies below, state whether or not it satisfies the necessary conditions for the integral test. Include a plot of the function that mimics the terms of the series. For those that satisfy the conditions, apply the integral test to determine if the given series converges or diverges. For those that do not satisfy the conditions, simply state that the integral test cannot be usedand use the direct comparison test.
- a
-
- b
-
- c
-



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2019-09-09
![]() , where
, where ![]() is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing
is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing ![]() as a function of n, it is usually not possible to find sums by directly using the definition.
as a function of n, it is usually not possible to find sums by directly using the definition.
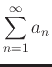 and
and
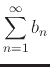 .
.
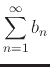 converges, then
converges, then
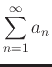 converges also.
converges also.
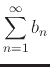 diverges, then
diverges, then
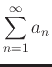 diverges also.
diverges also.
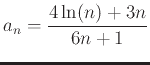 in Maple as a function of
in Maple as a function of