


Next: About this document
Up: Taylor Series
Previous: Maple Commands for Taylor
- 1.
- For each of the following functions, give the fifth-order Taylor polynomial at the point indicated. Then plot the polynomial and the function on the same graph, using an interval of length 2L centered at the given point.
- (a)
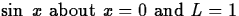
- (b)
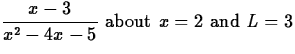 .
.- (c)
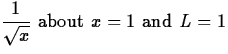 .
.- (d)
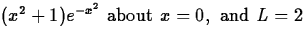 .
.
- 2.
- Plot several degrees of Taylor polynomial of
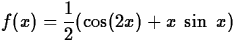 about x = 0. For each, give the interval on which the polynomial is close to the function f(x). You should decide how close is ``close to f(x)." One way to measure the interval is to plot the absolute value of the difference between the function and the Taylor polynomial.
What happens to the interval as the degree of the polynomial gets larger?
about x = 0. For each, give the interval on which the polynomial is close to the function f(x). You should decide how close is ``close to f(x)." One way to measure the interval is to plot the absolute value of the difference between the function and the Taylor polynomial.
What happens to the interval as the degree of the polynomial gets larger?
- 3.
- Consider the power series
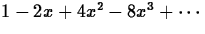 . What rational function does this power series represent? Describe what happens as larger degree Taylor polynomials are plotted against the function on the interval [0,2].
. What rational function does this power series represent? Describe what happens as larger degree Taylor polynomials are plotted against the function on the interval [0,2].
Due: Lab Time on September 29 or 30.
Roger Yin-Man Lui
9/20/1997
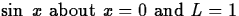
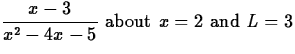 .
.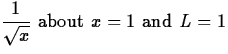 .
.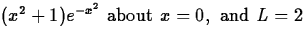 .
.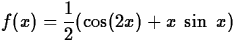 about x = 0. For each, give the interval on which the polynomial is close to the function f(x). You should decide how close is ``close to f(x)." One way to measure the interval is to plot the absolute value of the difference between the function and the Taylor polynomial.
What happens to the interval as the degree of the polynomial gets larger?
about x = 0. For each, give the interval on which the polynomial is close to the function f(x). You should decide how close is ``close to f(x)." One way to measure the interval is to plot the absolute value of the difference between the function and the Taylor polynomial.
What happens to the interval as the degree of the polynomial gets larger?