Exercises

Use Maple to work these problems.

1.

Plot the rose 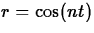$r = \cos(nt)$ for at least four consecutive integer values of n (but don't hand in more than four consecutive plots).

(a)

For a given n, how many petals does the rose have?

(b)

For a given n, what interval of t values should be used to trace out the entire curve without retracing any part of it?

(c)

For a given n, what is the area of one petal of the rose?

2.

Consider the polar coordinate plots of the curve $r = 2 - 3 sin(t), t \geq 0$

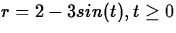
(a)

Plot the graph starting from t = 0 and report t each time the curve intersects the coordinate axes or returns to the origin. Do this until the graph forms a closed-loop.

(b)

The graph now consists of two closed loop. Find the area of the region bounded by the inner-loop.

(c)

Find the area of the region bounded between the two loops.

3.

Hand in an interesting plot of your own making. Use exponentials, powers of trig functions, whatever. Just create something unusual.