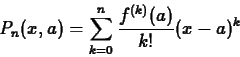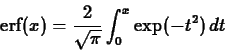Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to introduce you to
Taylor polynomial approximations to functions, including some
applications.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp ~bfarr/Taylor_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Taylor_start.mws, and go through it
carefully. Then you can start working on the exercises.
The idea of the Taylor polynomial approximation of order 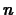 at
at
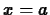 , written
, written 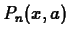 , to a smooth function
, to a smooth function 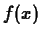 is to require
that
is to require
that 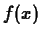 and
and 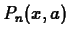 have the same value at
have the same value at 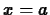 and,
furthermore, that their derivatives at
and,
furthermore, that their derivatives at 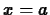 must match up to order
must match up to order
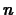 . For example the Taylor polynomial of order three for
. For example the Taylor polynomial of order three for 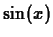 at
at
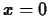 would have to satisfy the conditions
would have to satisfy the conditions
You should check for yourself that the cubic polynomial satisfying
these four conditions is
The general form of the Taylor polynomial approximation of order 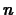 to
to 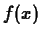 is given by the following
is given by the following
Theorem 1
Suppose that
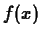
is a smooth function in some open interval
containing
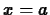
. Then the
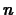
th degree Taylor polynomial of the
function
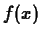
at the point
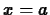
is given by
We will be seeing this formula a lot, so it
would be good for you to memorize it now! The notation
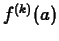 is used in the definition to stand for the value of the
is used in the definition to stand for the value of the
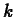 -th derivative of
-th derivative of 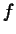 at
at 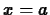 . That is,
. That is,
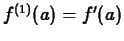 ,
,
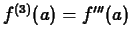 , and so on. By convention,
, and so on. By convention,
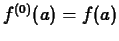 . Note that
. Note that 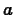 is fixed and so the derivatives
is fixed and so the derivatives 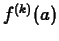 are
just numbers. The following easier theorem should help you to see
where the formula comes from.
are
just numbers. The following easier theorem should help you to see
where the formula comes from.
Theorem 2
Suppose
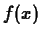
is a smooth function in some open interval
containing
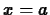
and that
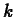
is a positive integer. Then
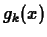
defined by
satisfies
To measure how well a Taylor Polynomial approximates the function over
a specified interval ![$[c,d]$](img23.gif) , we define the tolerance
, we define the tolerance 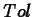 of
of
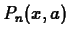 to be the maximum of the absolute error
to be the maximum of the absolute error
over the interval ![$[c,d]$](img23.gif) . The Getting started worksheet has
examples of how to compute and plot the absolute error.
. The Getting started worksheet has
examples of how to compute and plot the absolute error.
- For the following functions and base points, determine what
minimum order is required so that the Taylor polynomial approximates the
function to within a tolerance of
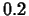 over the given
interval. Include explanations how you got your answers in your report.
over the given
interval. Include explanations how you got your answers in your report.
-
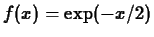 , base point
, base point 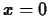 , interval
, interval ![$[-4,4]$](img28.gif) .
.
-
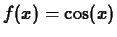 , base point
, base point 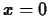 , interval
, interval ![$[0,4\pi ]$](img30.gif) .
.
-
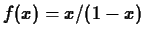 , base point
, base point 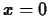 , interval
, interval ![$[-0.9,0.9]$](img32.gif) .
.
-
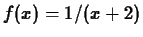 , base point
, base point 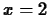 , interval
, interval ![$[-1.5, 3.5]$](img35.gif) .
.
- Prove Theorem 2. Remember that an example is
not a proof! (Note - this should be done by hand. part of using Maple
is knowing when not to use it.)
- For the third function in exercise 1,
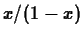 , consider the
Taylor polynomial with base point
, consider the
Taylor polynomial with base point 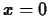 . Can you choose the order so that the
Taylor polynomial is a good approximation (within
. Can you choose the order so that the
Taylor polynomial is a good approximation (within 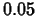 , say) to
, say) to
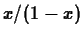 at
at 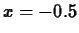 ? How about at
? How about at 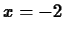 ? Discuss the difference in
the behavior of the Taylor polynomials at these two points. Can you
divide the real line up into parts, one where the approximation is
good and the others where it is bad?
? Discuss the difference in
the behavior of the Taylor polynomials at these two points. Can you
divide the real line up into parts, one where the approximation is
good and the others where it is bad?
- You know that the derivative of
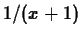 is
is 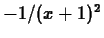 . Can you
find a relationship between the derivative of the
. Can you
find a relationship between the derivative of the 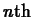 order
Taylor polynomial with base point
order
Taylor polynomial with base point 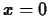 for
for 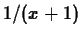 and and a Taylor
polynomial of some order with base point
and and a Taylor
polynomial of some order with base point 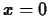 for
for 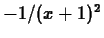 ?
?
- You know that the indefinite integral of
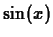 is
is
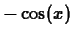 . Can you find a relationship between the indefinite
integral of the
. Can you find a relationship between the indefinite
integral of the 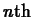 order
Taylor polynomial with base point
order
Taylor polynomial with base point 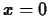 for
for 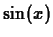 and and a Taylor
polynomial of some order with base point
and and a Taylor
polynomial of some order with base point 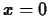 for
for 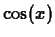 ? (Hint
- your answer should be yes.)
? (Hint
- your answer should be yes.)
- One of the applications of Taylor polynomials is in
approximating integrals. In the first lab, we encountered the error
function
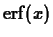 , which is defined by
, which is defined by
The idea of using Taylor polynomials to approximate the integral is to
replace the 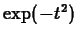 with its Taylor polynomial, which can be easily
integrated. Can you find the minimum order required to approximate
with its Taylor polynomial, which can be easily
integrated. Can you find the minimum order required to approximate
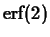 to within an accuracy of
to within an accuracy of 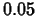 ? Use zero for the base
point of the Taylor polynomials.
? Use zero for the base
point of the Taylor polynomials.



Next: About this document ...
Up: lab_template
Previous: lab_template
William W. Farr
2000-11-22
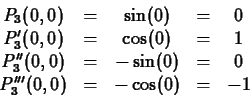
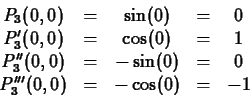
![]() to
to ![]() is given by the following
is given by the following