


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to introduce you to the notion
of improper integral and to give you practice with this concept by
using it to prove convergence or divergence of integrals involving
unbounded integrands or unbounded intervals or both.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory by going to your computer's Start menu and choose run. In the run field type:
\\storage\academics\math\calclab
when you hit enter, you can then choose MA1023 and then choose the worksheet
Improper_int_start_B14.mw
Remember to immediately save it in your own home directory. Once you've copied and saved the worksheet, read through the background on the internet and the background of the worksheet before starting the exercises.
Our basic theorem for
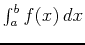 is that the integral
exists if
is that the integral
exists if 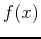 is continuous on the closed interval
is continuous on the closed interval ![$[a,b]$](img3.png) . We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on
. We have
actually gone beyond this theorem a few times,
and integrated functions that were bounded
and had a finite number of jump discontinuities on ![$[a,b]$](img3.png) .
However, we don't have any theory to help us deal with integrals
.
However, we don't have any theory to help us deal with integrals
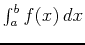 involving one or more of the following.
involving one or more of the following.
- Functions
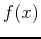 , for example rational functions, that have
vertical asymptotes in
, for example rational functions, that have
vertical asymptotes in ![$[a,b]$](img3.png) (or are not bounded on
(or are not bounded on ![$[a,b]$](img3.png) ).
).
- Integrals where the interval
![$[a,b]$](img3.png) is unbounded, for example
intervals like
is unbounded, for example
intervals like 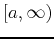 ,
, ![$(-\infty, b]$](img5.png) , or
, or
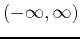 .
.
We have already seen at least one example of the problems you can run
into if the function is unbounded. Recall the clearly absurd result
that is obtained by blindly applying the FTOC. The second type of
problem, where the interval of integration is unbounded, occurs often
in applications of calculus, such as the Laplace and Fourier
transforms used to solve differential equations. It also occurs in
testing certain kinds of infinite series for convergence or
divergence, as we will learn later.
We start with the following definition.
To see how to handle the problem of an unbounded integrand, we start
with the following special cases.
Definition 2
Suppose that 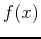 is continuous on
is continuous on 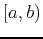 , but
, but
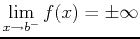 . Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
. Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
Definition 3
Suppose that 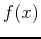 is continuous on
is continuous on ![$(a,b]$](img14.png) , but
, but
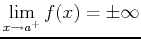 . Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
. Then we define
provided that the limit on the right-hand side exists and is finite,
in which case we say the integral converges and is equal to the value
of the limit. If the limit is infinite or doesn't exist, we say the
integral diverges or fails to exist and we cannot compute it.
Cases where 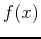 has an infinite discontinuity only at an interior
point
has an infinite discontinuity only at an interior
point 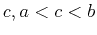 are handled by writing
are handled by writing
and using the definitions to see if the integrals on the right-hand
side exist. If both exist then the integral on the left-hand
side exists. If either of the integrals on the right-hand side
diverges, then
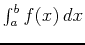 does not exist.
does not exist.
Here is a simple example using Maple to show that
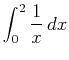 doesn't exist.
doesn't exist.
> ex1 := int(1/x,x=a..2);
> limit(ex1,a=0,right);
The example above used the right option to limit
because the right-hand limit was needed. If you need a left-hand
limit, use the left option in the limit command. Maple can usually do the limit within the int command.
> int(1/x,x=0..2);
These are handled in a similar fashion by using limits. The definition
we need the most is given below.
Definition 4
Suppose 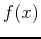 is continuous on the unbounded interval
is continuous on the unbounded interval 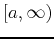 .
Then we define
provided the limit on the right-hand side exists and is finite, in
which case we say the integral converges and and is equal to the value
of the limit. If the limit is infinite or fails to exist we say the
integral diverges or fails to exist.
.
Then we define
provided the limit on the right-hand side exists and is finite, in
which case we say the integral converges and and is equal to the value
of the limit. If the limit is infinite or fails to exist we say the
integral diverges or fails to exist.
The other two cases are handled similarly. You are asked to provide
suitable definitions for them in one of the exercises.
Using the definition for
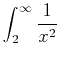 .
.
> ex2:=int(1/x^2,x=2..a);
> limit(ex2,a=infinity);
This command shows that Maple takes the limit definition into account in the int command.
> int(1/x^2,x=2..infinity);
- The gamma function is an example of an improper integral often used to approximate non-integer factorials and is defined below:
- A)
- Verify that
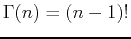 for
for 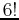 .
.
- B)
- Verify that
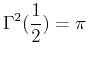
- C)
- Verify Euler's reflection formula:
You may need to use the
 command.
command.
- Determine which of the regions described below have finite area.
- A)
- The region below
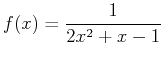 , above the
, above the  axis, over the interval
axis, over the interval 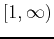 .
.
- B)
- The region below
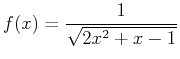 , above the
, above the 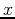 axis, over the interval
axis, over the interval 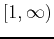 .
.
- C)
- The region below
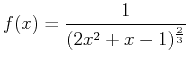 , above the
, above the 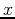 axis, over the interval
axis, over the interval 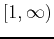 .
.
- Evaluate the following integral in Maple by splitting the range of integration into two ranges and completing two improper integrals. Be sure to use limits for each integral.
- Recall from Calculus II how to compute the volume and surface area of a solid of revolution. The formula for volume and surface area of
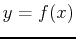 rotated about the
rotated about the 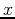 -axis over the interval
-axis over the interval
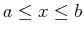 is given by:
is given by:
- (A)
- Find the volume of the solid obtained by revolving the curve
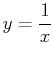 about the x-axis, between
about the x-axis, between 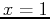 and
and 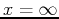 . Then find the volume of the solid by revolving the curve
. Then find the volume of the solid by revolving the curve
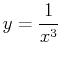 about the x-axis, between
about the x-axis, between 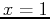 and
and 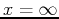 .
.
- (B)
- Find the surface area of each solid of revolution.
- (C)
- Is it possible to have a finite volume but an infinite surface area?



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2014-11-06
![]() has an infinite discontinuity only at an interior
point
has an infinite discontinuity only at an interior
point ![]() are handled by writing
are handled by writing
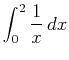 doesn't exist.
doesn't exist.
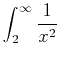 .
.
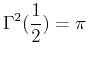
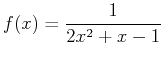 , above the
, above the 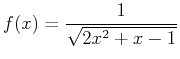 , above the
, above the 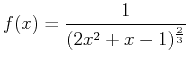 , above the
, above the 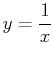 about the x-axis, between
about the x-axis, between 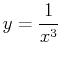 about the x-axis, between
about the x-axis, between