


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
This lab introduces you to the concept of convergence of sequences and series
with an application of geometric series involving a model for a drug being
given to a patient at regular intervals. As the drug is broken down by the
body, its concentration in the bloodstream decreases. However, it doesn't
disappear completely before the next dose is given. This means that
there is a tendency for the average drug concentration to increase
over time. It turns out that a geometric series is the key to
understanding how high the concentration can go.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory by going to your computer's Start menu and choose run. In the run field type:
\\storage\academics\math\calclab
when you hit enter, you can then choose MA1023 and then choose the worksheet
Seq_series_drug_start_B14.mw
Remember to immediately save it in your own home directory. Once you've copied and saved the worksheet, read through the background on the internet and the background of the worksheet before starting the exercises.
An infinite sequence is a list of numbers defined by the formula 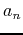 where
where 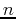 is the set of positive integers
is the set of positive integers 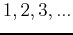 . A sequence is said to converge if the numbers in the in the list approach a single value as
. A sequence is said to converge if the numbers in the in the list approach a single value as 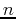 approaches
approaches 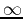 . If the numbers in the list increase or decrease without bound as
. If the numbers in the list increase or decrease without bound as 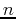 gets larger, then we say that the sequence diverges.
gets larger, then we say that the sequence diverges.
An infinite series is the sum of an infinite sequence. More precisely, the sum of an infinite series is defined as the limit of the sequence of the partial sums of the terms of the series, provided this limit exists. If no finite limit exists, then we say that the series is divergent.
The sum of an infinite series is defined as
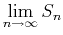 , where
, where 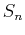 is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing
is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing 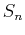 as a function of n, it is not always possible to find sums by directly using the definition.
as a function of n, it is not always possible to find sums by directly using the definition.
In this section, we describe an exponential decay model for the
concentration of a drug in a patient's bloodstream. We assume that the drug
is administered intravenously, so that the concentration of the drug
in the bloodstream jumps almost immediately to its highest level. The
concentration of the drug then decays exponentially. If we use 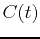 to represent the concentration at time t, and
to represent the concentration at time t, and 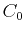 to represent the
concentration just after the first dose is administered then our exponential
decay model would be given by
to represent the
concentration just after the first dose is administered then our exponential
decay model would be given by
where 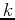 is the decay constant, and is a property of the particular
drug being used. It is usually obtained experimentally. The Getting Started worksheet has examples of how to compute
is the decay constant, and is a property of the particular
drug being used. It is usually obtained experimentally. The Getting Started worksheet has examples of how to compute 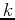 from
experimental data.
from
experimental data.
Now suppose that an additional dose of the drug is given to the
patient. Since we are assuming that when the drug is
administered it is diffused so rapidly throughout the bloodstream
that, for all
practical purposes, it reaches its highest concentration
instantaneously, we would see a jump in the concentration of the drug
when the new dose is given, as shown in the graph below.
![\includegraphics[height=4.0in]{drugfig1.ps}](img15.png)
After the additional dose is given, the concentration again decays over time.
A problem facing physicians is the fact that for most drugs, there is
a concentration, 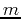 , below which the drug is ineffective and a
concentration,
, below which the drug is ineffective and a
concentration, 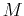 , above which the drug is dangerous. Thus the
physician would like the have the concentration
, above which the drug is dangerous. Thus the
physician would like the have the concentration 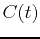 satisfy
satisfy
This requirement helps determine the initial dose of a drug and when
the next dose should be administered. For example, the first dose
should never raise the concentration above 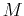 . That is, we must have
. That is, we must have
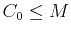 . To get a handle on the time between doses, we can
calculate the maximum possible time between doses. That is, suppose an
initial
dose is given such that the
concentration immediately after the dose is
. To get a handle on the time between doses, we can
calculate the maximum possible time between doses. That is, suppose an
initial
dose is given such that the
concentration immediately after the dose is 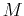 , the maximum
safe dose. If we calculate the time at which the concentration has
decayed to
, the maximum
safe dose. If we calculate the time at which the concentration has
decayed to 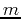 , then this gives the maximum time interval between
doses. This gives us an upper bound on the time between doses. The
worksheet contains examples of this kind of calculation. Note
that many factors could be important in
determining the time between doses that is actually used, including
practical considerations like
hospital schedules and shift changes.
, then this gives the maximum time interval between
doses. This gives us an upper bound on the time between doses. The
worksheet contains examples of this kind of calculation. Note
that many factors could be important in
determining the time between doses that is actually used, including
practical considerations like
hospital schedules and shift changes.
We next consider what happens if equal doses of the drug are given at
regular time intervals. Recall that a drug has a maximum safe
concentration, 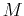 , and a minimum effective concentration,
, and a minimum effective concentration, 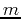 . We say
that a treatment program of equal, regularly-spaced doses is safe and
effective if the concentration
. We say
that a treatment program of equal, regularly-spaced doses is safe and
effective if the concentration 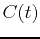 of the drug satisfies
of the drug satisfies
during the treatment.
In the first part of this lab, we presented
the expression
for the concentration of the drug after the first dose.
This expression is valid as long as only a single dose is
given. However, suppose that at 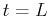 a second dose is given and that
the amount of the drug administered is the same as the first
dose. According to our model, the concentration will jump immediately
by an amount equal to
a second dose is given and that
the amount of the drug administered is the same as the first
dose. According to our model, the concentration will jump immediately
by an amount equal to 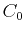 when the second dose is given. However,
when the second dose is given, there is still some of the drug in the
bloodstream remaining from the first dose. This means that to compute
the concentration just after the second dose, we have to add the value
when the second dose is given. However,
when the second dose is given, there is still some of the drug in the
bloodstream remaining from the first dose. This means that to compute
the concentration just after the second dose, we have to add the value
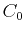 to the concentration remaining from the first dose. During the
time between the second and third doses, the concentration decays
exponentially from this value. To find the concentration after the
third dose, we would have to repeat this process, but now we have
contributions from the first and second doses to include.
to the concentration remaining from the first dose. During the
time between the second and third doses, the concentration decays
exponentially from this value. To find the concentration after the
third dose, we would have to repeat this process, but now we have
contributions from the first and second doses to include.
We can calculate the
concentration just before the second dose is administered by setting
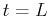 in our equation
in our equation
to get
where by 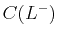 we mean the
we mean the
Now, when the second dose is administered the concentration jumps by
an increment 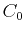 so that the concentration just after the second
dose is given is
so that the concentration just after the second
dose is given is
The concentration then decays from this value according to our
exponential decay rule, but with a slight twist. The twist is that the
``initial'' concentration is at 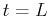 , instead of the more familiar
case of
, instead of the more familiar
case of 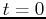 . One way to handle this is to write the exponential term
as
. One way to handle this is to write the exponential term
as
so that at 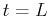 , the exponent is
, the exponent is 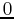 . If we do this, then we can
write the concentration as a function of time as
. If we do this, then we can
write the concentration as a function of time as
This function is only valid after the second dose is administered and
before the third dose is given. That is, for 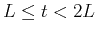 .
.
Now, suppose that a third dose of the drug is given at 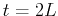 . The
concentration just before the third dose is given is
. The
concentration just before the third dose is given is 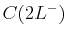 , which
is
, which
is
which we can also write as
When the third dose is given, the concentration would jump again by
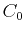 and the concentration just after the third dose would be
and the concentration just after the third dose would be
This process can be continued and leads to the following two formulas.
The first is the concentration just before the
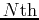 dose of the drug. This is
dose of the drug. This is
The second result we need is the concentration just after the
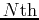 dose, which is
dose, which is
At this point, you are probably wondering how geometric series fit
into this lab. The answer should be a lot clearer if we define a
parameter 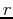 by
by
Note that 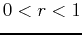 , since
, since 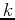 and
and 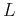 are both positive constants.
The properties of the exponential function can be used to show that
are both positive constants.
The properties of the exponential function can be used to show that
where 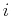 is a non-negative integer.
We can write our two fromulas for the concentration just
before and after the
is a non-negative integer.
We can write our two fromulas for the concentration just
before and after the 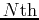 dose in terms of
dose in terms of 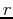 as
as
and
where the formula for the partial sum of a geometric series has been
used to obtain the last equality in each of the equations above.
Now, suppose a treatment program is to be continued indefinitely. The
formulas above show that 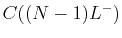 and
and 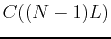 both increase
with
both increase
with  . This means that the minimum concentration is the
concentration just before the second dose or
. This means that the minimum concentration is the
concentration just before the second dose or
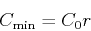
and that the maximum concentration occurs just after the last
dose. Thus we have that
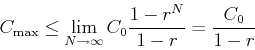
- Write the sequence
 as a function. List the first fifteen terms.
as a function. List the first fifteen terms.
- Plot the first fifteen terms. Does it appear to converge or diverge? If it seems to converge, to what does it converge?
- Calculate the limit of the sequence as
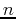 approaches
approaches 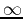 . Is your answer close to your approximation above?
. Is your answer close to your approximation above?
- Write a function for the sum of the sequence. List the first ten terms of the sequence of partial sums.
- Plot the at least the first ten terms of the sequence of partial sums (You may want to restrict the
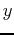 range to
range to
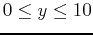 ). Does it appear that the series converges or diverges? If it seems to converge, to what does it converge?
). Does it appear that the series converges or diverges? If it seems to converge, to what does it converge?
- Calculate the limit of the series as
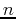 approaches
approaches 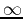 .
.
- Suppose that for a certain drug, which we'll refer to as drug A,
the following results were
obtained. Immediately after the drug was administered, the
concentration was 3.3 mg/ml. Six hours later, the concentration had
dropped to 1.55 mg/ml. Determine the value of
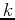 for this drug.
for this drug.
- Consider drug A, assuming that doses are
given every six hours, or
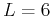 . Compute the minimum initial dose
. Compute the minimum initial dose
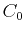 that will keep the concentration above the minimum effective
level for the first six hours, i.e before the second dose is given.
that will keep the concentration above the minimum effective
level for the first six hours, i.e before the second dose is given.
- Consider drug A again, with doses to be given
every six hours. Can you find a dose
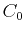 such that the concentration
stays below
such that the concentration
stays below 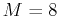 and above
and above  for at least 72 hours?
for at least 72 hours?
- Trials of another drug, call it drug B, produced the following data. The concentration just after the drug was administered was 6 mg/ml and 5 hours later the concentration was 1.2 mg/ml. If the maximum safe concentration is 10 mg/ml and the minimum effective concentration is 2 mg/ml, find one set of values of
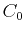 and
and 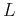 that provide a safe and effective treatment program. (Hint: Copy commands from part 1, 2, and 3 of this exercise and make the appropriate changes. You should also change the variable name for the constant
that provide a safe and effective treatment program. (Hint: Copy commands from part 1, 2, and 3 of this exercise and make the appropriate changes. You should also change the variable name for the constant 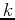 from
from 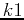 to
to 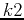 .)
.)
- Suppose that new research with drug A shows that the maximum safe level is
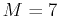 and the minimum effective dose is
and the minimum effective dose is  Can you find values of
Can you find values of 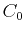 and
and 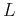 that produce a safe and effective treatment program? Try at least two sets of values of
that produce a safe and effective treatment program? Try at least two sets of values of 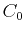 and
and 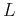 .
.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2014-11-13
![]() , where
, where ![]() is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing
is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing ![]() as a function of n, it is not always possible to find sums by directly using the definition.
as a function of n, it is not always possible to find sums by directly using the definition.
![\includegraphics[height=4.0in]{drugfig1.ps}](img15.png)
![]() , below which the drug is ineffective and a
concentration,
, below which the drug is ineffective and a
concentration, ![]() , above which the drug is dangerous. Thus the
physician would like the have the concentration
, above which the drug is dangerous. Thus the
physician would like the have the concentration ![]() satisfy
satisfy
![]() in our equation
in our equation
![]() . The
concentration just before the third dose is given is
. The
concentration just before the third dose is given is ![]() , which
is
, which
is
![]() dose of the drug. This is
dose of the drug. This is
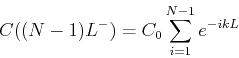
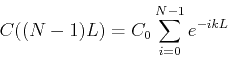
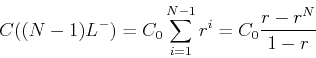
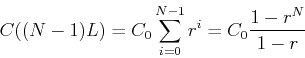
![]() and
and ![]() both increase
with
both increase
with ![]() . This means that the minimum concentration is the
concentration just before the second dose or
. This means that the minimum concentration is the
concentration just before the second dose or
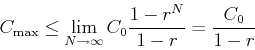
 as a function. List the first fifteen terms.
as a function. List the first fifteen terms.