


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to introduce you to a number of useful commands for working with vectors, including some applications. The commands come from the Maple linalg and CalcP7 packages which must be loaded before any of its commands can be used.
To assist you, there is a worksheet associated with this lab that you can copy into your home directory by going to your computer's start menu and choose run. In the run field type:
\\storage\academics\math\calclab
when you hit enter, you can then choose MA1023 and then choose the worksheet
Vector_start_B14.mw
Remember to immediately save it in your own home directory. Once you've copied and saved the worksheet, read through the background on the internet and the background of the worksheet before starting the exercises.
The commands below are some of the most basic vector commands. Some examples using these commands can be found in the Getting Started Worksheet. More examples can be found in the Help screens for each command.
innerprod
Computes the dot product (also known as the inner product) of two vectors.
crossprod
Computes the cross product of two vectors.
evalm
Evaluates expressions involving vectors (and matrices).
norm
Computes the norm, or length, of a vector.
If 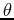 is the angle between the vectors
is the angle between the vectors 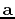 and
and 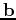 , then
, then
 .
.
The vector projection of 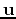 onto
onto 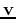 or the component of
or the component of 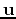 in the direction of
in the direction of 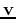 can be found using the following formula:
can be found using the following formula:
The scalar component of 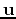 in the direction of
in the direction of 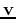 can be found using the following formula:
can be found using the following formula:
The triangle created by connecting the terminal ends of the vectors 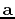 and
and 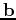 in standard form has area =
in standard form has area =
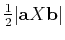 .
.
A unit vector perpendicular to the plane containing points 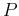 ,
, 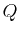 and
and 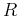 is given by
is given by
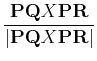 .
.
- Given the vectors
![${\bf a} = [2.14,6.02,-3.83]$](img14.png) and
and
![${\bf b} = [3.45,-5.28,-1.74]$](img15.png) , and
, and
![${\bf c} = [1.86,6.24,1.87]$](img16.png) , use Maple to compute the numeric value of the following expressions, if possible. For those that cannot be computed because they make no sense, please explain what is wrong.
, use Maple to compute the numeric value of the following expressions, if possible. For those that cannot be computed because they make no sense, please explain what is wrong.
-
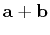
-
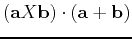
-
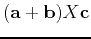
-
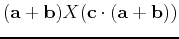
- Find the angle between each of the vectors above.
- Find a vector
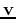 perpendicular to
perpendicular to 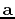 such that
such that
where
![${\bf a} = [4,-2 \pi]$](img22.png) and
and
![${\bf b} = [\alpha,\beta]$](img23.png) . Then show that
. Then show that 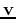 and
and 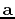 are perpendicular.
are perpendicular.
- Find the equation of the line through the point
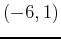 and parallel to the vector
and parallel to the vector
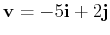 . Plot the line and vector on the same graph.
. Plot the line and vector on the same graph.
- For the vectors
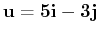 and
and
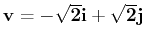 , find the vector projection of
, find the vector projection of 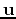 onto
onto 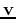 and the scalar component of
and the scalar component of 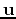 in the direction of
in the direction of 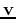 .
.
- Find the area of the triangle with vertices
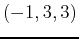 ,
, 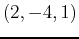 and
and 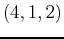 . (Hint: Shift the triangle to the origin by representing two of the sides of the triangles with vectors in standard form.)
Also, find a unit vector perpendicular to the plane containing these three points.
. (Hint: Shift the triangle to the origin by representing two of the sides of the triangles with vectors in standard form.)
Also, find a unit vector perpendicular to the plane containing these three points.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2014-12-10
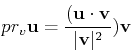
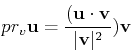
![]() ,
, ![]() and
and ![]() is given by
is given by
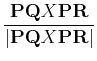 .
.