


Next: Maple Commands
Up: lab_template
Previous: Purpose
Subsections
There are many times in math, science, and engineering that coordinate
systems other than the familiar one of Cartesian coordinates are
convenient. In this lab, we consider one of the most common and useful
such systems, that of polar coordinates.
The main reason for using polar coordinates is that they can be used
to simply describe regions in the plane that would be very difficult
to describe using Cartesian coordinates. For example, graphing the
circle 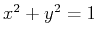 in Cartesian coordinates requires two functions -
one for the upper half and one for the lower half. In polar
coordinates, the same circle has the very simple representation
in Cartesian coordinates requires two functions -
one for the upper half and one for the lower half. In polar
coordinates, the same circle has the very simple representation 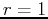 .
.
These are three types of well-known graphs in polar coordinates. The
table below will allow you to identify the graphs in the exercises.
| Name |
Equation |
| cardioid |
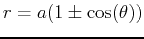 or or
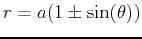 |
| limaçon |
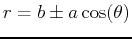 or or
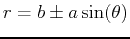 |
| rose |
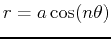 or or
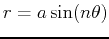 |
Finding where two graphs in Cartesian coordinates intersect is
straightforward. You just set the two functions equal and solve for
the values of 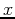 . In polar coordinates, the situation is more
difficult. Most of the difficulties are due to the following considerations.
. In polar coordinates, the situation is more
difficult. Most of the difficulties are due to the following considerations.
- A point in the plane can have more than one representation in
polar coordinates. For example,
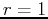 ,
, 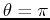 is the same
point as
is the same
point as 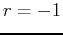 ,
, 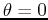 . In general a point in the plane can have
an infinite number of representations in polar coordinates, just by
adding multiples of
. In general a point in the plane can have
an infinite number of representations in polar coordinates, just by
adding multiples of 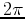 to
to 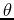 . Even if you restrict
. Even if you restrict 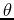 a point in the plane can have several different representations.
a point in the plane can have several different representations.
- The origin is determined by
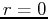 . The angle
. The angle 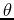 can have
any value.
can have
any value.
These considerations can make finding the intersections of two graphs in polar
coordinates a difficult task. As the exercises demonstrate, it
usually requires a combination of plots and solving equations to find
all of the intersections.



Next: Maple Commands
Up: lab_template
Previous: Purpose
Dina J. Solitro-Rassias
2015-11-12
![]() in Cartesian coordinates requires two functions -
one for the upper half and one for the lower half. In polar
coordinates, the same circle has the very simple representation
in Cartesian coordinates requires two functions -
one for the upper half and one for the lower half. In polar
coordinates, the same circle has the very simple representation ![]() .
.