


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to introduce you to
Taylor polynomial approximations to functions, including some
applications.
To assist you, there is a worksheet associated with this lab that
contains examples similar to some of the exercises. On your Maple screen go to File - Open then type the following in the white rectangle:
\\storage\academics\math\calclab\MA1023\Taylor_powerseries_start_B16.mw
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read through the exercises, start up Maple, load the worksheet, and go through it carefully. Then you can start working on the exercises.
The idea of the Taylor polynomial approximation of order 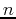 at
at
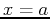 , written
, written 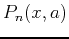 , to a smooth function
, to a smooth function 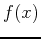 is to require
that
is to require
that 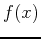 and
and 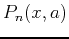 have the same value at
have the same value at 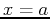 .
Furthermore, their derivatives at
.
Furthermore, their derivatives at 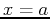 must match up to order
must match up to order
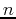 . For example the Taylor polynomial of order three for
. For example the Taylor polynomial of order three for 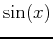 at
at
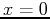 would have to satisfy the conditions
would have to satisfy the conditions
You should check for yourself that the cubic polynomial satisfying
these four conditions is
The general form of the Taylor polynomial approximation of order 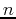 to
to 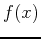 is given by the following
is given by the following
Theorem 1
Suppose that 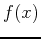 is a smooth function in some open interval
containing
is a smooth function in some open interval
containing 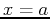 . Then the
. Then the 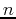 th degree Taylor polynomial of the
function
th degree Taylor polynomial of the
function 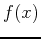 at the point
at the point 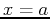 is given by
is given by
We will be seeing this formula a lot, so it
would be good for you to memorize it now! The notation
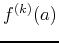 is used in the definition to stand for the value of the
is used in the definition to stand for the value of the
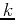 -th derivative of
-th derivative of 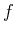 at
at 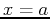 . That is,
. That is,
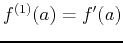 ,
,
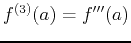 , and so on. By convention,
, and so on. By convention,
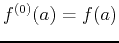 . Note that
. Note that 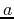 is fixed and so the derivatives
is fixed and so the derivatives 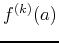 are
just numbers. That is, a Taylor polynomial has the form
are
just numbers. That is, a Taylor polynomial has the form
which you should recognize as a power series that has been truncated.
The Ratio Test for convergence of a series can be thought of as a measurement of how fast the series is increasing or decreasing. This can be found by looking at the ratio
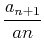 as
as
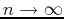 .
Given the series
.
Given the series
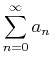 , suppose that
, suppose that
Given the series
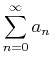 , suppose that
, suppose that
Then
- the series converges if
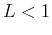 ,
,
- the series diverges if
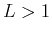 ,
,
- the test is inconclusive if
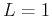 .
.
The radius of convergence of a series can usually be found by using the ratio test:
Next, you would need to solve for the interval of 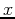 values such that
values such that 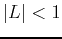 .
.
To measure how well a Taylor Polynomial approximates the function over
a specified interval ![$[c,d]$](img29.png) , we define the tolerance
, we define the tolerance 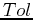 of
of
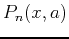 to be the maximum of the absolute error
to be the maximum of the absolute error
over the interval ![$[c,d]$](img29.png) .
.
To use the Taylor and TayPlot commands you need to load the CalcP7 package.
>with(CalcP7);
The exponential function can be approximated at a base point zero with a polynomial of order four using the following command.
>Taylor(exp(x),x=0,4);
You might want to experiment with changing the order. To see
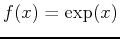 and its fourth order polynomial use
and its fourth order polynomial use
>TayPlot(exp(x),x=0,{4},x=-4..4);
This plots the exponantial and three approximating polynomials.
>TayPlot(exp(x),x=0,{2,3,4},x=-2..2);
Notice that the further away from the base point, the further the polynomial diverges from the function. the amount the polynomial diverges i.e. its error, is simply the difference of the function and the polynomial.
>plot(abs(exp(x)-Taylor(exp(x),x=0,3)),x=-2..2);
This plot shows that in the domain x from -2 to 2 the error around the base point is zero and the error is its greatest at x = 2 with a difference of over one. You can experiment with the polynomial orders to change the accuracy. If your work requires an error of no more than 0.2 within a given distance of the base point then you can plot your accuracy line y = 0.2 along with the difference of the function and the Taylor approximation polynomial.
>plot([0.2,abs(exp(x)-Taylor(exp(x),x=0,3))],x=-2..2,y=0..0.25);
We knew this would have some of its error well above 0.2. Change the order from three to four. As you can see there are still some values in the domain close to x = 2 whose error is above 0.2. Now try an order of 5. Is the error entirely under 0.2 between x = -2 and x = 2? Larger orders will work as well but order five is the minimum order that will keep the error under 0.2 within the given domain.
- Use Maple to find the interval of convergence for the following series
- a)
-
- b)
-
- Find the power series for each function listed below about
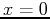 and then determine the interval of
and then determine the interval of 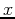 values over which the series converges.
values over which the series converges.
-
-
-
- For the function,
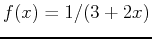 , use the TayPlot command to plot the function and multiple Taylor polynomial approximations of various orders with base point
, use the TayPlot command to plot the function and multiple Taylor polynomial approximations of various orders with base point 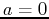 on the same graph over the interval
on the same graph over the interval
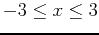 ; use a y-range from
; use a y-range from 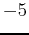 to
to 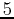 .
.
- a)
- If you increase the order of the Taylor polynomial, can you get a good approximation at
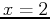 ?
?
- b)
- Estimate the interval of convergence based on the plot and compare to the actual interval of convergence as done in the previous exercise.
- For the following functions and base points, determine what
minimum order is required so that the Taylor polynomial approximates the
function to within a tolerance of
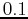 over the given
interval.
over the given
interval.
- a)
-
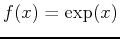 , base point
, base point 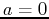 , interval
, interval ![$[-2,2]$](img45.png) .
.
- b)
-
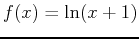 , base point
, base point 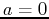 , interval
, interval ![$[-0.9,0.9]$](img47.png) .
.
- c)
-
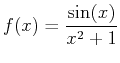 , base point
, base point 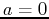 , interval
, interval ![$[-0.9,0.9]$](img47.png) .
.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2016-12-01
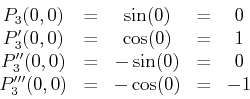
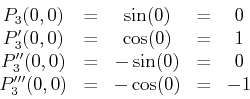
![]() to
to ![]() is given by the following
is given by the following
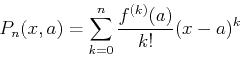
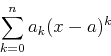
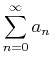 , suppose that
, suppose that 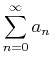 , suppose that
, suppose that
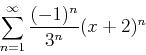
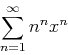
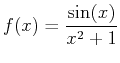 , base point
, base point