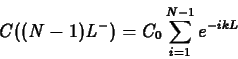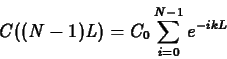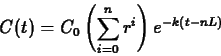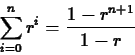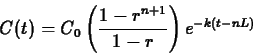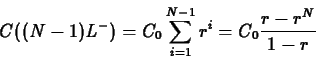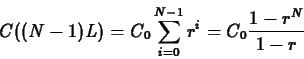Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
This lab concerns a model for a drug being given to a patient at
regular intervals. As the drug is broken down by the body, its
concentration in the bloodstream decreases. However, it doesn't
disappear completely before the next dose is given. This means that
there is a tendency for the average drug concentration to increase
over time. It turns out that a geometric series is the key to
understanding how high the concentration can go.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp ~bfarr/Drug_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read through the exercises,
start up Maple, load
the worksheet Drug_start.mws, and go through it
carefully. Then you can start working on the exercises.
In this section, we describe an exponential decay model for the
concentration of a drug in a patient's bloodstream. We assume that the drug
is administered intravenously, so that the concentration of the drug
in the bloodstream jumps almost immediately to its highest level. The
concentration of the drug then decays exponentially. If we use 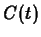 to represent the concentration at time t, and
to represent the concentration at time t, and 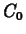 to represent the
concentration just after the first dose is administered then our exponential
decay model would be given by
to represent the
concentration just after the first dose is administered then our exponential
decay model would be given by
where 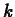 is the decay constant, and is a property of the particular
drug being used. It is usually obtained experimentally. The worksheet
Drug_start.mws has examples of how to compute
is the decay constant, and is a property of the particular
drug being used. It is usually obtained experimentally. The worksheet
Drug_start.mws has examples of how to compute 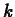 from
experimental data.
from
experimental data.
Now suppose that an additional dose of the drug is given to the
patient. Since we are assuming that when the drug is
administered it is diffused so rapidly throughout the bloodstream
that, for all
practical purposes, it reaches its highest concentration
instantaneously, we would see a jump in the concentration of the drug
when the new dose is given, as shown in the graph below.
![\includegraphics[height=4.0in]{drugfig1.ps}](img5.gif)
After an additional dose, the concentration again decays over time.
A problem facing physicians is the fact that for most drugs, there is
a concentration, 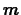 , below which the drug is ineffective and a
concentration,
, below which the drug is ineffective and a
concentration, 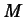 , above which the drug is dangerous. Thus the
physician would like the have the concentration
, above which the drug is dangerous. Thus the
physician would like the have the concentration 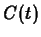 satisfy
satisfy
This requirement helps determine the initial dose of a drug and when
the next dose should be administered. For example, the first dose
should never raise the concentration above 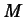 . That is, we must have
. That is, we must have
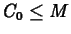 . To get a handle on the time between doses, we can
calculate the maximum possible time between doses. That is, suppose an
initial
dose is given such that the
concentration immediately after the dose is
. To get a handle on the time between doses, we can
calculate the maximum possible time between doses. That is, suppose an
initial
dose is given such that the
concentration immediately after the dose is 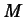 , the maximum
safe dose. If we calculate the time at which the concentration has
decayed to
, the maximum
safe dose. If we calculate the time at which the concentration has
decayed to 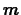 , then this gives the maximum time interval between
doses. This gives us an upper bound on the time between doses. The
worksheet contains examples of this kind of calculation. Note
that many factors could be important in
determining the time between doses that is actually used, including
practical considerations like
hospital schedules and shift changes.
, then this gives the maximum time interval between
doses. This gives us an upper bound on the time between doses. The
worksheet contains examples of this kind of calculation. Note
that many factors could be important in
determining the time between doses that is actually used, including
practical considerations like
hospital schedules and shift changes.
We next consider what happens if equal doses of the drug are given at
regular time intervals. Recall that a drug has a maximum safe
concentration, 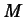 , and a minimum effective concentration,
, and a minimum effective concentration, 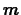 . We say
that a treatment program of equal, regularly-spaced doses is safe and
effective if the concentration
. We say
that a treatment program of equal, regularly-spaced doses is safe and
effective if the concentration 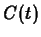 of the drug satisfies
of the drug satisfies
during the treatment.
In the first part of this lab, we presented
the expression
for the concentration of the drug after the first dose.
This expression is valid as long as only a single dose is
given. However, suppose that at 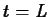 a second dose is given and that
the amount of the drug administered is the same as the first
dose. According to our model, the concentration will jump immediately
by an amount equal to
a second dose is given and that
the amount of the drug administered is the same as the first
dose. According to our model, the concentration will jump immediately
by an amount equal to  when the second dose is given. However,
when the second dose is given, there is still some of the drug in the
bloodstream remaining from the first dose. This means that to compute
the concentration just after the second dose, we have to add the value
when the second dose is given. However,
when the second dose is given, there is still some of the drug in the
bloodstream remaining from the first dose. This means that to compute
the concentration just after the second dose, we have to add the value
 to the concentration remaining from the first dose. During the
time between the second and third doses, the concentration decays
exponentially from this value. To find the concentration after the
third dose, we would have to repeat this process, but now we have
contributions from the first and second doses to include.
to the concentration remaining from the first dose. During the
time between the second and third doses, the concentration decays
exponentially from this value. To find the concentration after the
third dose, we would have to repeat this process, but now we have
contributions from the first and second doses to include.
We can calculate the
concentration just before the second dose is administered by setting
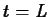 in our equation
in our equation
to get
where by 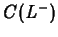 we mean the
we mean the
Now, when the second dose is administered the concentration jumps by
an increment 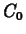 so that the concentration just after the second
dose is given is
so that the concentration just after the second
dose is given is
The concentration then decays from this value according to our
exponential decay rule, but with a slight twist. The twist is that the
``initial'' concentration is at 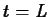 , instead of the more familiar
case of
, instead of the more familiar
case of 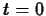 . One way to handle this is to write the exponential term
as
. One way to handle this is to write the exponential term
as
so that at 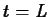 , the exponent is
, the exponent is 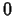 . If we do this, then we can
write the concentration as a function of time as
. If we do this, then we can
write the concentration as a function of time as
This function is only valid after the second dose is administered and
before the third dose is given. That is, for 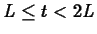 .
.
Now, suppose that a third dose of the drug is given at 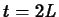 . The
concentration just before the third dose is given is
. The
concentration just before the third dose is given is 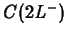 , which
is
, which
is
which we can also write as
When the third dose is given, the concentration would jump again by
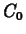 and the concentration just after the third dose would be
and the concentration just after the third dose would be
Finally, an expression for the concentration that would be valid after
the third dose is administered but before the fourth dose would be
This process can be continued to get expressions for the concentration
for any number of equal, regularly-spaced doses. Here is a general
formula that is valid for
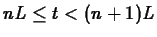
It must be noted that the value of 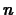 in this equation is not the
number of doses that have been given. Instead, it is one less than the
number of doses given. Mathematically, we can express
in this equation is not the
number of doses that have been given. Instead, it is one less than the
number of doses given. Mathematically, we can express 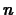 in the
following way. If we divide through the inequality
in the
following way. If we divide through the inequality
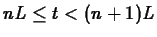 by the positive value
by the positive value 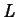 we obtain the following.
we obtain the following.
That is, 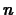 is the integer part of
is the integer part of 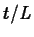 . The function that returns
the integer part of a number occurs frequently in Mathematics and is
called the greatest integer function. It is usually denoted by square
brackets. That is, for any real number
. The function that returns
the integer part of a number occurs frequently in Mathematics and is
called the greatest integer function. It is usually denoted by square
brackets. That is, for any real number 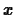 ,
, ![$[x]$](img33.gif) is read as the greatest integer in
is read as the greatest integer in 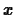 . For example,
. For example, ![$[2.9999] = 2$](img34.gif) .
.
There are two special cases for the concentration formula that we will
need later. The first is the concentration just before the
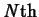 dose of the drug. This is
dose of the drug. This is
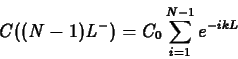
The second result we need is the concentration just after the
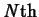 dose, which is
dose, which is
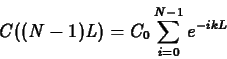
At this point, you are probably wondering how geometric series fit
into this lab. The answer should be a lot clearer if we define a
parameter 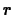 by
by
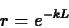
Note that 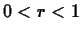 , since
, since 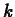 and
and 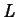 are both positive constants.
The properties of the exponential function can be used to show that
are both positive constants.
The properties of the exponential function can be used to show that
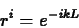
where 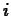 is a non-negative integer. This means that we can write our
formula for
is a non-negative integer. This means that we can write our
formula for 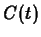 as
as
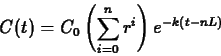
where, as before, this formula is valid for
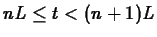 .
Noting that the sum in the formula is a partial sum of a geometric
series, we use the
formula
.
Noting that the sum in the formula is a partial sum of a geometric
series, we use the
formula
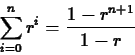
to write 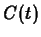 as follows.
as follows.
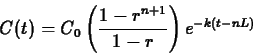
We also can write our two special cases for the concentration just
before and after the 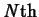 dose in terms of
dose in terms of 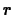 as
as
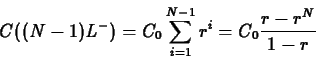
and
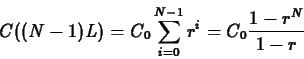
- Suppose that for a certain drug, which we'll refer to as drug B,
the following results were
obtained. Immediately after the drug was administered, the
concentration was 3.3 mg/ml. Six hours later, the concentration had
dropped to 1.55 mg/ml. Determine the value of
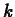 for this drug.
for this drug.
- Suppose that for drug B, the maximum
safe level is
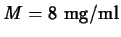 and the minimum effective level is
and the minimum effective level is
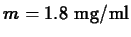 . What is the maximum possible time between doses
for this drug?
. What is the maximum possible time between doses
for this drug?
- Consider drug B, assuming that doses are
given every six hours, or
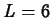 . Compute the minimum initial dose
. Compute the minimum initial dose
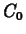 that will keep the concentration above the minimum effective
level for the first six hours, i.e before the second dose is given.
that will keep the concentration above the minimum effective
level for the first six hours, i.e before the second dose is given.
- Consider drug B again, with doses to be given
every six hours. Can you find a dose
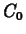 such that the concentration
stays below
such that the concentration
stays below 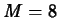 and above
and above 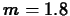 for at least 48 hours?
for at least 48 hours?
- Trials of another drug, which we'll call drug C, produced the
following data. The
concentration just after the drug was administered was 6 mg/ml and 5
hours later the concentration was 1.2 mg/ml. Find the value of
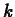 for
this drug and label it k2 in your worksheet. If the maximum safe
concentration is 10 mg/ml and the minimum effective concentration is 2
mg/ml, find one set of values of
for
this drug and label it k2 in your worksheet. If the maximum safe
concentration is 10 mg/ml and the minimum effective concentration is 2
mg/ml, find one set of values of 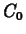 and
and 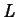 that provide a safe and
effective treatment program. Make sure you explain your answers.
that provide a safe and
effective treatment program. Make sure you explain your answers.
- Suppose that new research on drug C from the previous exercise
indicates that the values of
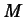 and
and 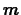 should be
should be 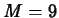 and
and 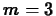 . Can you find values of
. Can you find values of 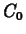 and
and 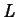 that produce a safe and effective treatment program? Try at
least two sets of values of
that produce a safe and effective treatment program? Try at
least two sets of values of 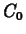 and
and 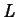 . If your values don't work,
then can you suggest a way to change the treatment program to make it
safe and effective?
. If your values don't work,
then can you suggest a way to change the treatment program to make it
safe and effective?
- Suppose a program of equal doses at regular intervals is to be
carried out indefinitely. What is the minimum value of the drug
concentration and when does it occur? This is a general question and
your answer should depend on
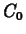 and
and 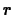 . Is there a maximum value
for the drug concentration? If not, is there an upper bound for the
drug concentration? Your answer here should also depend on
. Is there a maximum value
for the drug concentration? If not, is there an upper bound for the
drug concentration? Your answer here should also depend on 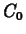 and
and
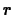 . (Note - this question is probably best answered using pencil and
paper. Part of using Maple is knowing when not to use it.)
. (Note - this question is probably best answered using pencil and
paper. Part of using Maple is knowing when not to use it.)



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2001-01-23
![\includegraphics[height=4.0in]{drugfig1.ps}](img5.gif)
![]() , below which the drug is ineffective and a
concentration,
, below which the drug is ineffective and a
concentration, ![]() , above which the drug is dangerous. Thus the
physician would like the have the concentration
, above which the drug is dangerous. Thus the
physician would like the have the concentration ![]() satisfy
satisfy
![]() in our equation
in our equation
![]() . The
concentration just before the third dose is given is
. The
concentration just before the third dose is given is ![]() , which
is
, which
is
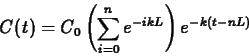
![]() dose of the drug. This is
dose of the drug. This is