


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to give you practice with parametric
curves in the plane and in visualizing parametric curves as
representing motion.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp /math/calclab/MA1023/Parametric_start_C08.mws ~/My_Documents
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Parametric_start_C08.mws, and go through it
carefully. Then you can start working on the exercises.
A parametric curve in the plane is defined as an ordered
pair, 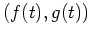 , of functions, with
, of functions, with 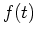 representing the
representing the 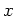 coordinate and
coordinate and 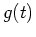 the
the 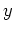 coordinate. Parametric curves arise
naturally as the solutions of differential equations and often
represent the motion of a particle or a mechanical system. They
also often arise in studying oscillations in electrical circuits.
coordinate. Parametric curves arise
naturally as the solutions of differential equations and often
represent the motion of a particle or a mechanical system. They
also often arise in studying oscillations in electrical circuits.
For example, neglecting air resistance, the position of a projectile
fired from the origin at an initial speed of
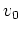 and angle of inclination
and angle of inclination 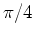 is given by the parametric
equations
is given by the parametric
equations
where 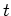 is time and
is time and 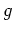 is the acceleration due to gravity.
is the acceleration due to gravity.
To help you to visualize parametric curves as representing motion, a
Maple routine called ParamPlot has been written. It uses the
Maple animate command to actually show the particle moving along
its trajectory. You actually used this command before for the lab
on polar coordinates. Examples are in the Getting Started
worksheet.
The graph of a parametric curve may not have a slope at every point on
the curve. When the slope exists, it must be given by the formula
from class.
It is clear that this formula doesn't make sense if
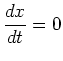 at some particular value of
at some particular value of 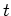 . If
. If
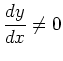 at that same value of
at that same value of 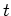 , then it turns out the
graph has a vertical tangent at that point. If both
, then it turns out the
graph has a vertical tangent at that point. If both
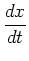 and
and
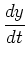 are zero at some
value of
are zero at some
value of 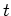 , then the curve often doesn't have a tangent line at that
point. What you see instead is a sharp corner, called a cusp.An
example of this appears in the first exercise.
, then the curve often doesn't have a tangent line at that
point. What you see instead is a sharp corner, called a cusp.An
example of this appears in the first exercise.
As mentioned above, parametric curves often represent the motion of a
particle or mechanical system. As we will see in class, when we think
of a parametric curve as representing motion, we need a way to measure
the distance traveled by the particle. This distance is given by the
arc length, 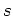 , of a curve. For a parametric curve
, of a curve. For a parametric curve 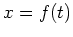 ,
,
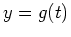 , the arc length of the curve for
, the arc length of the curve for
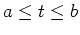 is given
below.
is given
below.
While the concept of arc length is very useful for the theory of
parametric curves, it turns out to be very difficult to compute in all
but the simplest cases.
There are a variety of ways to work with parametric equations in Maple. There is an animation command that shows how the graph is plotted over t. For example the parabola 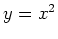 can be written parametrically in different ways two of them are
can be written parametrically in different ways two of them are ![$[t,t^2]$](img22.png) and
and ![$[-t,t^2]$](img23.png)
>with(plots):
>with(CalcP7):
>implicitplot(x^2=y,x=-2..2,y=0..4,scaling=constrained);
>ParamPlot([t,t^2],t=-2..2,scaling=constrained);
>ParamPlot([-t,t^2],t=-2..2,scaling=constrained);
The ParamPlot command produces an animated plot. To see the animation, execute the command and then click on the plot region below to make the controls appear in the Context Bar just above the worksheet window.
To enter a function parametrically
>f:=t->[t*cos(3*t),t^2];
>VPlot(f(t),t=-2*Pi..2*Pi);
- The cycloid is a famous example of a parametric curve having
several important applications. Use the ParamPlot command to
animate the cycloid
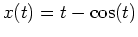 ,
,
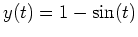 over the
interval
over the
interval
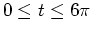 . The sharp points in the graph are called cusps. Use the formula for the slope of a parametric curve to find values of
. The sharp points in the graph are called cusps. Use the formula for the slope of a parametric curve to find values of 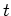 for where these cusps occur and explain why it makes sense for the cusps to occur only at these values of
for where these cusps occur and explain why it makes sense for the cusps to occur only at these values of 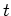 . That is, verify that the curve has a slope at all other values of
. That is, verify that the curve has a slope at all other values of 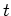 in the interval.
in the interval.
- The family of parametric curves
where
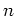 and
and 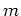 are positive integers, is an example of what is called a
Lissajous figure. Use a parametric plot to plot the three cases
are positive integers, is an example of what is called a
Lissajous figure. Use a parametric plot to plot the three cases
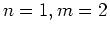 ,
, 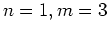 and
and 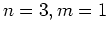 and describe what you see.
and describe what you see.
- The parametric description
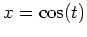 ,
, 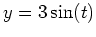 ,
,
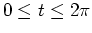 is the ellipse
is the ellipse
First show that the two are the same shape by plotting them parametrically and with the command implicitplot.
Use the formula above to set up an integral for the arc length of the
ellipse. You should find that Maple can't do the integral
exactly. This is because this integral can't be done analytically. You can get a numerical approximation to the integral by putting an evalf command on the outside of the int command.
- Consider the family of parametric curves
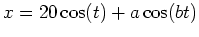 and
and
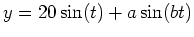 , where
, where 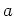 and
and 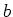 are positive constants, with
are positive constants, with 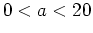 and
and 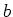 is a positive integer. Use a paramentric plot to test the following properties of this family.
is a positive integer. Use a paramentric plot to test the following properties of this family.
- i
- The curve only has loops in it if
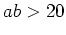 . (Plot the example in the worksheet to see what loops look like.)
. (Plot the example in the worksheet to see what loops look like.)
- ii
- If the curve has loops in it, the number of loops is
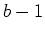 .
.
- iii
- The curve has cusps if
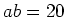 and there are exactly
and there are exactly 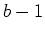 of them.
Use at least two sets of values of
of them.
Use at least two sets of values of 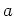 and
and 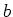 to test each property. Don't forget that
to test each property. Don't forget that 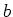 has to be an integer and
has to be an integer and 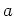 should be smaller than 20.
should be smaller than 20.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2008-02-12
![]() and angle of inclination
and angle of inclination ![]() is given by the parametric
equations
is given by the parametric
equations
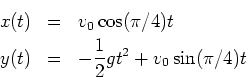
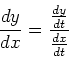
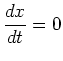 at some particular value of
at some particular value of 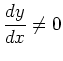 at that same value of
at that same value of