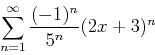Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to learn how to define sequences and series using Maple as well as observe their plots and test for convergence.
To assist you, there is a worksheet associated with this lab that
contains examples similar to some of the exercises.On your Maple screen go to File - Open then type the following in the white rectangle:
\\storage\academics\math\calclab\MA1023\Series_start_C16.mw
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read through the exercises, start up Maple, load the worksheet, and go through it carefully. Then you can start working on the exercises.
The Ratio Test for convergence of a series can be thought of as a measurement of how fast the series is increasing or decreasing. This can be found by looking at the ratio
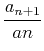 as
as
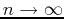 .
.
Given the series
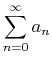 , suppose that
, suppose that
Then
- the series converges if
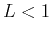 ,
,
- the series diverges if
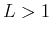 ,
,
- the test is inconclusive if
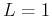 .
.
The radius of convergence of a series can usually be found by using the ratio test:
Next, you would need to solve for the interval of 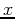 values such that
values such that 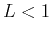 . Below is an example of how you could use Maple to find the interval of convergence for the power series for the function
. Below is an example of how you could use Maple to find the interval of convergence for the power series for the function
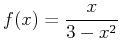 .
.
> series(x/(3-x^2),x=0,12);
> a:=n->x^(2*n+1)/3^(n+1);
> l:=simplify(limit(abs(a(n+1)/a(n)),n=infinity));
> solve(abs(x)^2/3<1,x);
From this, we can conclude that the interval of convergence is
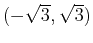 .
.
- For the following functions and base points, determine what
minimum order is required so that the Taylor polynomial approximates the
function to within a tolerance of
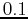 over the given
interval.
over the given
interval.
- a)
-
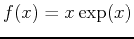 , base point
, base point 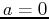 , interval
, interval ![$[-2,2]$](img15.png) .
.
- b)
-
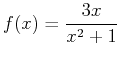 , base point
, base point 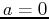 , interval
, interval ![$[-0.9,0.9]$](img17.png) .
.
- c)
-
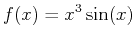 , base point
, base point 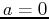 , interval
, interval ![$[0 ,4\pi]$](img19.png) .
.
- Use Maple to find the interval of convergence for the following series
- Find the power series for each function listed below about
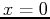 and then determine the interval of
and then determine the interval of 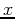 values over which the series converges.
values over which the series converges.
-
-



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2016-02-02
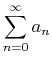 , suppose that
, suppose that
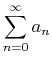 , suppose that
, suppose that
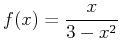 .
.
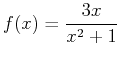 , base point
, base point