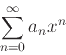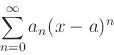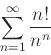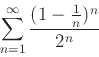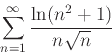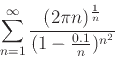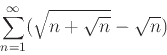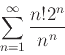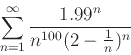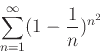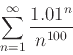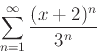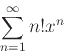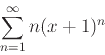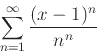Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to learn how to determine convergence of series using Maple as well as introduce you to power series and their radius of convergence.
To assist you, there is a worksheet associated with this lab that
contains examples similar to some of the exercises. On your Maple screen go to File - Open then type the following in the white rectangle:
\\storage\academics\math\calclab\MA1023\Series_start_C19.mw
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read through the exercises, start up Maple, load the worksheet, and go through it carefully. Then you can start working on the exercises.
An infinite series is the sum of an infinite sequence. More precisely, the sum of an infinite series is defined as the limit of the sequence of the partial sums of the terms of the series 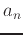 , provided this limit exists. If no finite limit exists, then we say that the series is divergent.
, provided this limit exists. If no finite limit exists, then we say that the series is divergent.
The sum of an infinite series is defined as
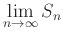 , where
, where 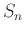 is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing
is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing 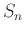 as a function of n, it is usually not possible to find sums by directly using the definition.
as a function of n, it is usually not possible to find sums by directly using the definition.
So, if we can generally not work from the definition, what can be done? There are several convergence tests that provide us with some needed tools. These are tests that tell us if a series converges, but in the case that the series does converge, does not tell us the sum of the series.
The series
diverges if
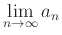 is non-zero or does not exist.
is non-zero or does not exist.
For Direct Comparison, consider the series
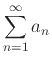 and
and
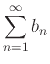 .
.
- If
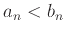 for
for 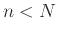 , where
, where 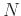 is some integer and
is some integer and
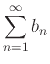 converges, then
converges, then
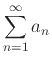 converges also.
converges also.
- If
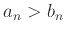 for
for 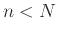 , where
, where 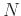 is some integer and
is some integer and
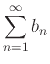 diverges, then
diverges, then
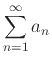 diverges also.
diverges also.
For Limit Comparison, consider the same series above
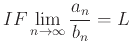
- And if
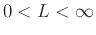 , then
, then
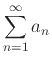 and
and
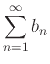 both converge or both diverge.
both converge or both diverge.
- If
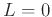 and
and
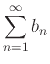 converges, then
converges, then
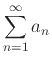 converges also.
converges also.
- If
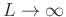 and
and
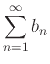 diverges, then
diverges, then
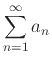 diverges also.
diverges also.
The Integral Test for convergence is a method used to test convergence of an infinite series of nonnegative terms.
The series
converges if and only if the integral
is finite, where 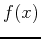 is a positive, non-increasing and continuous function defined on the interval
is a positive, non-increasing and continuous function defined on the interval 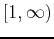 and
and 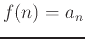 an for all
an for all 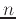 .
.
The Ratio Test for convergence of a series can be thought of as a measurement of how fast the series is increasing or decreasing. This can be found by looking at the ratio
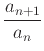 as
as
 .
Given the series
.
Given the series
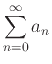 , suppose that
, suppose that
Then
- the series converges if
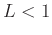 ,
,
- the series diverges if
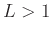 ,
,
- the test is inconclusive if
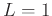 .
.
A power series about  has the form
has the form
and a power series about  has the form
has the form
where 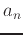 are the constant coefficients of the powers of
are the constant coefficients of the powers of 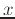 .
.
The radius of convergence of a power series can usually be found by using the Tatio test:
Next, you would need to solve for the interval of 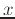 values such that
values such that 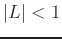 . Remember that power series always converge:
. Remember that power series always converge:
- If
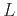 exists and is non-zero, the power series converges absolutely on some interval
exists and is non-zero, the power series converges absolutely on some interval 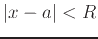 .
.
- If
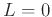 , the power series converges for all
, the power series converges for all 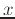 .
.
- If
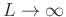 , the power series converges only at
, the power series converges only at 
- Use any convergence test to determine if each of the following series converges or diverges and explain your answer.
-
-
-
-
-
-
-
-
-
- Use Maple to find the radius and interval of convergence for the each of the following power series
-
-
-
-



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2019-01-30
![]() , where
, where ![]() is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing
is the partial sum of the first n terms of the series. However, because of the algebraic difficulty of expressing ![]() as a function of n, it is usually not possible to find sums by directly using the definition.
as a function of n, it is usually not possible to find sums by directly using the definition.
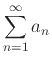 and
and
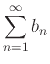 .
.
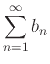 converges, then
converges, then
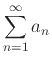 converges also.
converges also.
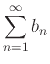 diverges, then
diverges, then
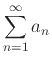 diverges also.
diverges also.
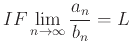
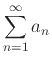 and
and
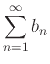 both converge or both diverge.
both converge or both diverge.
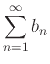 converges, then
converges, then
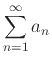 converges also.
converges also.
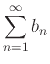 diverges, then
diverges, then
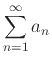 diverges also.
diverges also.
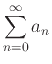 , suppose that
, suppose that