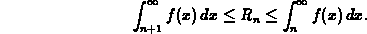This test is the content of the following theorem, which we'll prove in class.
That is, if the improper integral converges then the series converges and if the improper integral diverges, the series diverges. The proof of this theorem rests on the inequality
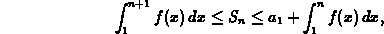
where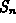 
is the n-th partial sum of the series. This inequality
is obtained by thinking of 
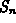as a Riemann sum, just like we did in
class to prove the divergence of the harmonic series.
To help you see where the inequality comes from, we'll consider our
example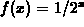 
and n=5.
We can visualize the connection between the sums and the integrals by
using some
plotting commands from the student package. The following
command plots the function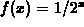 
and a left-endpoint
rectangular approximation to the integral of 
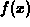from x=1 to
x=6.
> with(student):
> leftbox(f(x),x=1..6,5);
If you add up the areas of the five rectangles, you get
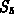. Clearly, the sum of the areas of the rectangles is greater than
the area under the curve, so we have the following inequality.
Next, consider the plot generated by the following command.
> rightbox(f(x),x=1..5,4);
The sum of the areas of the rectangles is a right-endpoint
approximation to the integral of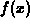 
from x=1 to x=5. It should
be clear that the sum of the areas of the rectangle is smaller than
the integral. Note also that the sum of the areas is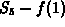 
,
that is, it is missing the first term. Thus, what we have is that
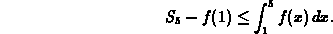
Adding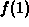 
to both sides of the inequality and recognizing that
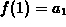, we have
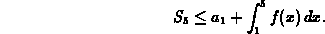
This shows that the inequality holds for n=5. It isn't too hard to generalize it to arbitrary n.
A similar procedure can be used to estimate the error term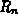 
,
defined by
in terms of integrals as
