


Next: About this document
Up: Infinite Series and
Previous: Example
- Using the Integral Test, determine whether the following
infinite series converge or diverge:
-

-

-

-

- The items in this problem refer to the following series:

- Determine the appropriate function
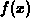 for this series and then
calculate the appropriate integral. Explain why this shows that the
series converges.
for this series and then
calculate the appropriate integral. Explain why this shows that the
series converges.
- Plot the partial sums
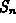 for
for 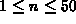 . Why does this plot
show that
. Why does this plot
show that 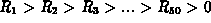 ? Is it always true that
? Is it always true that
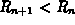 for this series?
for this series?
- How many terms of the series must be added together to guarantee
that the remainder is no more than
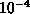 ?
?
- Consider the harmonic series

- Use the integral test to show that this series diverges.
- Compute and/or plot partial sums,
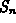 , of this series for various
values of n. How large must n be for the partial sum to be greater
than 20? Greater than 50? Do you think that if you just computed
partial sums and didn't use the integral test you would think the
series converged?
, of this series for various
values of n. How large must n be for the partial sum to be greater
than 20? Greater than 50? Do you think that if you just computed
partial sums and didn't use the integral test you would think the
series converged?
William W. Farr
Wed Jan 24 13:38:10 EST 1996

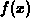 for this series and then
calculate the appropriate integral. Explain why this shows that the
series converges.
for this series and then
calculate the appropriate integral. Explain why this shows that the
series converges.
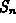 for
for 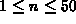 . Why does this plot
show that
. Why does this plot
show that 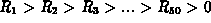 ? Is it always true that
? Is it always true that
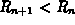 for this series?
for this series?
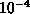 ?
?

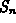 , of this series for various
values of n. How large must n be for the partial sum to be greater
than 20? Greater than 50? Do you think that if you just computed
partial sums and didn't use the integral test you would think the
series converged?
, of this series for various
values of n. How large must n be for the partial sum to be greater
than 20? Greater than 50? Do you think that if you just computed
partial sums and didn't use the integral test you would think the
series converged?



