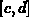 , we define the tolerance Tol of
, we define the tolerance Tol of
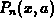 to be the maximum of
to be the maximum of
To measure how well a Taylor Polynomial approximates the function over
a specified interval 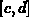 , we define the tolerance Tol of
, we define the tolerance Tol of
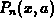 to be the maximum of
to be the maximum of

over the interval 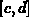 . You can actually see how the error of a
Taylor polynomial varies over an interval with a Maple command like
. You can actually see how the error of a
Taylor polynomial varies over an interval with a Maple command like
> plot(abs(sin(x)-Taylor(sin(x),x=0,3)),x=-1..1);
For this example, the tolerance, Tol, is about 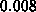 , which you can
find out by looking at the graph.
, which you can
find out by looking at the graph.
Now suppose you were asked to determine the order required so that the
Taylor polynomial approximation to 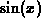 had a tolerance of
had a tolerance of
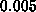 on the interval
on the interval 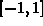 . One simple method for doing this
graphically is shown below.
. One simple method for doing this
graphically is shown below.
> plot(abs(sin(x)-Taylor(sin(x),x=0,3)),x=-1..1,y=0..0.005);
If you look at the plot, you see that the curve goes out of the plot on the top of the window. This means that the tolerance is not satisfied. If the order is increased to 5, as in the following example, then the curve goes out of the plot on the sides, meaning that the tolerance is satisfied.
> plot(abs(sin(x)-Taylor(sin(x),x=0,5)),x=-1..1,y=0..0.005);