

Next: About this document
Up: Taylor Polynomials
Previous: Accuracy and Tolerance
- For the following functions and base points, determine the smallest
order that is required so that the Taylor polynomial approximates the
function to within a tolerance of
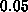 over the given
interval. Be sure to explain how you got your answers in your
report. This means including any plots that you used to make your conclusion.
over the given
interval. Be sure to explain how you got your answers in your
report. This means including any plots that you used to make your conclusion.
-
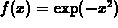 , a=0, interval
, a=0, interval 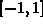 .
.
-
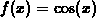 , a=0, interval
, a=0, interval 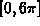 .
.
-
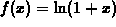 , a=0, interval
, a=0, interval 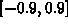 .
.
-
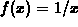 , a=1, interval
, a=1, interval 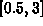 .
.
- Prove Theorem 2. Remember that an example is not a proof!
- For the third function in exercise 1,
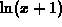 , consider the
Taylor polynomial about a=0. Can you choose the order so that the
Taylor polynomial is a good approximation (within
, consider the
Taylor polynomial about a=0. Can you choose the order so that the
Taylor polynomial is a good approximation (within 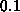 , say) to
, say) to
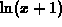 at x=2 ? How about at
at x=2 ? How about at
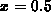 ? Discuss the difference in
the behavior of the Taylor polynomials at these two points. Can you
divide the real line up into two parts, one where the approximation is
good and one where it is bad?
? Discuss the difference in
the behavior of the Taylor polynomials at these two points. Can you
divide the real line up into two parts, one where the approximation is
good and one where it is bad?
Sean O Anderson
Tue Feb 6 14:48:55 EST 1996
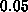 over the given
interval. Be sure to explain how you got your answers in your
report. This means including any plots that you used to make your conclusion.
over the given
interval. Be sure to explain how you got your answers in your
report. This means including any plots that you used to make your conclusion.
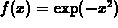 , a=0, interval
, a=0, interval 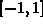 .
.
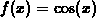 , a=0, interval
, a=0, interval 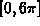 .
.
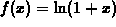 , a=0, interval
, a=0, interval 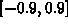 .
.
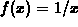 , a=1, interval
, a=1, interval 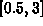 .
.
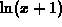 , consider the
Taylor polynomial about a=0. Can you choose the order so that the
Taylor polynomial is a good approximation (within
, consider the
Taylor polynomial about a=0. Can you choose the order so that the
Taylor polynomial is a good approximation (within 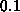 , say) to
, say) to
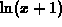 at x=2 ? How about at
at x=2 ? How about at
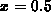 ? Discuss the difference in
the behavior of the Taylor polynomials at these two points. Can you
divide the real line up into two parts, one where the approximation is
good and one where it is bad?
? Discuss the difference in
the behavior of the Taylor polynomials at these two points. Can you
divide the real line up into two parts, one where the approximation is
good and one where it is bad?