Problem statement

A.

Each data set in Table 1 represents a different drug and a different initial dose. For each data set solve the differential equation and answer the following questions.

1. Sketch a graph of the concentration function; that is, graph the level of concentration vs. time. Assume concentrations are measured in milligrams per milliliter and time is measured in hours.

2. Predict the time when the blood becomes free of the drug, assuming no further doses are administered. Justify your answer.

3. Predict what the graph of the concentration level vs. time would look like if further doses of the drug were administered every six hours for forty-eight hours. Justify your answer.

B.

For this part, work with the general model. That is, let k be parameter whose value is not known, but use the exponential decay model described above.

1. If a constant dose, which raises the blood concentration instantaneously by a value of 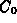every time it is administered, is given every L hours, derive formulas which give the values of the following two quantities.
   1. The drug concentration just before the 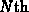dose of the drug is given.
   2. The drug concentration just after the 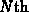dose of the drug is given.
   Your formulas should involve partial sums of geometric series. This may be easier to see if you define

   

   Physically, r is the factor by which the concentration of the drug is decreased during the time L between doses.

2. Based on your answer to the previous question, describe what would happen to the concentration level of the drug if it were administered indefinitely.

C.

A problem facing physicians is the fact that for most drugs, there is a concentration below which the drug will be ineffective and a concentration above which the drug will be dangerous (see Figure 2).

 
Figure 2: Safe drug concentration range

1. Suppose that for the drug in experiment 2, the minimum effective level is 0.75 mg per ml and the maximum safe level is 4.75 mg per ml. If the dose in the experiment is given every six hours, will the appropriate concentrations be maintained? Indefinitely? Justify your answer.

   If the answer is no, can you achieve a satisfactory long-run level just by adjusting the time between doses? Just by adjusting the dose? Justify your answer. (Assume there is a simple way to tell just how much substance must be administered in order to raise the concentration by any given amount. That is, you can answer this question by specifying how much the concentration of the drug in the blood needs to be raised on each dose.)

2. For this part, work with the general model. That is, treat k, 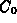, and L as parameters. Suppose that the concentration at which the drug becomes ineffective is m and that the concentration at which the drug becomes dangerous is M. Show that if the equation

   

   is satisfied the drug can be safely and effectively administered by giving the same dose at regularly spaced time intervals. That is, there is a dosage program that keeps the drug concentration above m and below M indefinitely.