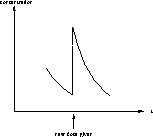
Figure 1: Drug concentration before and after a dose
The concentration in the blood resulting from a single dose of a drug normally decreases with time as the drug is eliminated from the body. In order to determine the exact pattern that the decrease follows, experiments are performed in which the drug concentrations in the blood are measured at various times after the drug is administered. The data are then checked against a hypothesized function relating the drug concentration to time.
For our problem, we will make the following assumption: namely that when the drug is administered, it is diffused so rapidly throughout the bloodstream that, for all practical purposes, it reaches its fullest concentration instantaneously. Thus, the concentration jumps from a low or zero level to a higher level in zero time. Visually, this represents a vertical jump on the graph of concentration vs. time (see Figure 1). This assumption is nearly justified for drugs that are administered intravenously, but not for drugs that are taken orally.
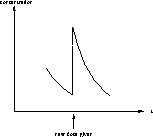
Figure 1: Drug concentration before and after a dose
A model which has been found to work fairly well in clinical trials is to assume that the rate at which the concentration is decreasing at time t is proportional to the concentration level at time t. This idea can be modeled by the differential equation

where y is the concentration of the drug in the blood at time t and k is a constant. Suppose a single dose of a certain drug is administered to a patient at time t=0, and that the blood concentration is measured immediately thereafter, and again after four hours. The results of two such experiments are given in Table 1 below.