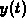This document describes some Maple commands that will be useful to you in working with the project. However, it doesn't tell you exactly how to use the commands described here for your project work - that is up to you.
The Maple commands described here can be used to more easily define functions for the drug concentration. The main difficulty is that the concentration is defined by different formulas in different time intervals. However, it turns out that by using the Maple sum and floor commands, the desired function can be defined rather simply.
In the project, a new dose of the drug is given every L hours. In
between doses, the concentration decays exponentially from its value
just after the dose is given to that just before the next dose is
given. That is, between doses the concentration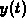 
behaves like
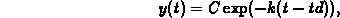
where td is the time at which the most recent dose was given, and
C is the concentration just after the most recent dose was given.
The problem is that both C and td depend on how many doses have
been given. One of the questions in the project asks you to derive a
formula for C, so you are on your own there. This document is
intended to help you understand how to calculate td and introduce
you to some Maple commands that will help you define the function
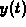in a simple manner.
Given a value of t, the time the last dose was given can be
calculated if we know the number of doses that have been given and the
time L between doses. For example, if only one dose has been given,
then the time of the most recent dose must be td = 0. If two doses
have been given, then the time of the most recent dose is td = L. In
general, you should be able to convince yourself that if N doses
have been given, then the time of the most recent dose is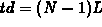 
.
Given a value of t, the number of doses, N given up to that time can be
calculated easily by dividing t by L, the time between doses,
taking the integer part of the result, and then adding 1 (for the
initial dose). For example, suppose that doses were being given every
4 hours. After 21 hours, the number of doses given can be
calculated to be 6 by taking the integer part of 
(
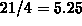=5) and adding 1. However, since what we really need to calculate td is
N-1 we can just divide t by L and take the integer
part of the result. The next section contains further mathematical
background and examples of Maple commands that will be useful to you.