Exercises

1. Consider . From your knowledge of trigonometry you should suspect that the sequence converges to . Use the solve command to solve the inequality

   

   for n when k = 0.004. When k = 0.0006. When k = 0.00005. Explain how these results support the belief that the limit is actually .

2. 1. Plot the first 30 terms of the sequence 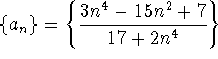. What behavior of the sequence is suggested by the graph? Check the value of 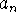for several values of n greater than 30. Make a guess for the value of the limit. What theorem about sequences assures us that, in fact, this sequence does converge?
   2. Construct an increasing sequence that is bounded above by 20 and has a limit L that satisfies the condition 10 < L < 20. Show a plot of your sequence. What is the limit of your sequence? Prove that your number is indeed the limit.
3. Use the Maple sum command to find for each of the following infinite series. Then use the limit command to find . What is the significance of this limit?

   1. 

   2. 

   3. 

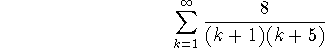
   4. Show how exercise 3.1 could have been done by hand.
4. Maple has several ways that can be used to try to find the sum of an infinite series. One such technique was used in exercise 3. Another method is explored in this exercise.
   1. Consider 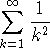. Work this by the technique of exercise 3. The sum looks a little strange; but take its limit anyway. Redo the problem (in a single step) by using the sum command to sum from 1 to infinity.
   2. Consider 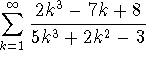. Try using the sum command to sum from 1 to infinity. What happens? Next use the technique of exercise 3. What theorem could have been used to anticipate the answer?
   3. Consider 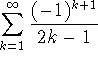. What happens when you use the technique of exercise 3 here? What happens if you sum from 1 to infinity? Which answer do you believe? Why?