Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for
![]()
![]()
![]()
Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
In Section 8.2 of the text the sum of an infinite series is defined as ![]() , where Sn is the partial sum of the first n terms of the series. However, because of the algebraic difficulty (often, impossibility) of expressing Sn as a function of n, it is usually not possible to find sums by directly using the definition.
, where Sn is the partial sum of the first n terms of the series. However, because of the algebraic difficulty (often, impossibility) of expressing Sn as a function of n, it is usually not possible to find sums by directly using the definition.
So, if we can generally not work from the definition, what can be done? The convergence tests of Sections 8.3, 8.4, 8.5 and 8.6 provide us with some needed tools. These are tests that tell us if a series converges, but - in the case the series does converge - do not tell us the sum of the series. Then, how do we find the sum? The answer is that we usually cannot find the sum. However, we can approximate the sum, S, by the partial sum Sn, for an appropriate value of n. But, what value of n will guarantee that S is, for instance, approximated by Sn to three decimal places?
For most of the tests there is not a good answer to this question. In many cases a heuristic approach is used - look at Sn for successive values of n until it seems that the third decimal place in the Sn will not change further. Note that there is no guarantee that this procedure will actually give the desired accuracy. For instance, it would be easy to be fooled by a slowly converging series.
For the convergent series ![]() , we define the remainder after n terms as
, we define the remainder after n terms as 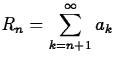 . It should be clear that S = Sn + Rn and that Rn is in fact the error when Sn is used to approximate S. As is usual in approximation arguments, we seek an upper bound on the absolute value of the error. The argument that is used to prove the integral test can be modified so as to establish the following bounds.
. It should be clear that S = Sn + Rn and that Rn is in fact the error when Sn is used to approximate S. As is usual in approximation arguments, we seek an upper bound on the absolute value of the error. The argument that is used to prove the integral test can be modified so as to establish the following bounds.
![]()
where f(i) = ai when i is a positive integer. Thus, under the assumption that ak > 0 for all k, we have
![]()
That is, we have a bound on the error arising by using Sn to approximate S.
Use the Maple command ?help to read more about the sum command. Note especially the use of single quotes when using sum.
Sometimes it may be advantageous to use Sum and value instead of just sum. The use of Sum enables you to check if you have typed the series correctly. As an example, look at
> Sum('1/2^k','k'=1..100);
> value(");
Also try these commands with "100" replaced by "infinity." When you use sum to find the value of some Sn, you will usually want to use it in conjunction with evalf.
> evalf(sum( ));Otherwise, in some cases, Maple will attempt to do exact arithmetic and the answer may be long enough to fill several screens.
Christine M Palmer