Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for
![]()
![]()
![]()
Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
So far, you have considered series whose terms were constants; for example the geometric series
![]()
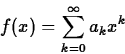
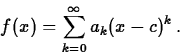
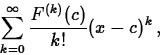
The Taylor series for F(x) at c is not necessarily equal to F(x) on the series's interval of convergence. (See the text, p. 555, for a counterexample.) However, if F(x) can be represented by a power series at c, the Taylor series must be the power series that does so. In practice the Taylor series does converge to the function for most functions of interest, so that the Taylor series for a function is an excellent way to work that function.
You have seen that a good strategy for working with infinite sums is to use a partial sum as an approximation, and to try to get a bound on the size of the remainder. This leads to the question of whether one can approximate a given function F(x) by using a partial sum of its Taylor series, a question which is answered by Taylor's theorem.
Theorem If f(x) and all its derivatives exist in an open interval containing c, then for each x in that interval, we may write
f(x) = Tn(x)+Rn(x)
where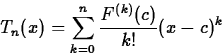
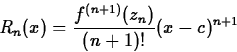
Observe that zn depends on x; hence Rn(x) is not a term of a Taylor polynomial.
Maple contains a built in function, taylor, for generating Taylor series. For example, the following maple command generates the first four terms of the Taylor series for the exponential function about x=0.5.
>taylor(exp(x),x=0.5,4);
Note the O((x-0.5)4) term at the end. This term represents the remainder function. The third argument of the taylor command corresponds to the order of the remainder term, not the degree of the Taylor polynomial printed out. Also, note that the presence of the remainder term prevents the output of the taylor command from being plotted or manipulated algebraically.
To overcome this obstacle, the CalcP package contains a slightly different command, Taylor (with a capital T). The output of the Taylor command is a polynomial that can be used in other expressions just like any other polynomial:
>with(CalcP):
>Taylor(exp(x),x=0.5,4);
>plot(",x=0..1);
Note that the third argument gives the degree of the Taylor polynomial output (unlike the first command, which gives the degree of the first term omitted).
For this lab, you will probably find the command Taylor to be more useful than the command taylor. We mention the first command because it is a standard Maple command.
A second useful command in the CalcP package is TayPlot. This command generates graphs of a function and several of its Taylor polynomials on the same plot.
>TayPlot(cos(x),x=0,{2,4,6},x=-Pi..Pi);
![]()
> plot(abs(sin(x)-Taylor(sin(x),x=0,3)),x=-1..1);
For this example, the tolerance, Tol, is about 0.008, which you can find out by looking at the graph.
Now suppose you were asked to determine the order required so that the
Taylor polynomial approximation to ![]() had a tolerance of
0.005 on the interval [-1,1]. One simple method for doing this
graphically is shown below.
had a tolerance of
0.005 on the interval [-1,1]. One simple method for doing this
graphically is shown below.
> plot(abs(sin(x)-Taylor(sin(x),x=0,3)),x=-1..1,y=0..0.005);
If you look at the plot, you see that the curve goes out of the plot on the top of the window. This means that the tolerance is not satisfied. If the order is increased to 5, as in the following example, then the curve goes out of the plot on the sides, meaning that the tolerance is satisfied.
> plot(abs(sin(x)-Taylor(sin(x),x=0,5)),x=-1..1,y=0..0.005);
So, by looking at this plot, you can conclude that a Taylor polynomial of degree five would approximate the function ![]() for any point in the interval
for any point in the interval ![]() to two decimal point accuracy.
to two decimal point accuracy.
Suppose that you were asked to check that this is true for any point in that interval, say x = 1 using the error bound. You would need to show that ![]() lies between two values that agree to "at least" two decimal places. This can be done by solving the inequality
lies between two values that agree to "at least" two decimal places. This can be done by solving the inequality 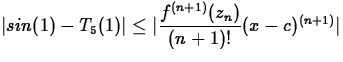 for
for ![]() . (In this example, n=5, c=0, x=1, and T5(1) is the fifth degree Taylor polynomial approximation to
. (In this example, n=5, c=0, x=1, and T5(1) is the fifth degree Taylor polynomial approximation to ![]() evaluated at x = 1.) The term on the right hand side of this inequality, the Taylor remainder term, needs to be maximized so that we know what the largest possible error would be. How do you maximize any quantity? You find its derivative, set it equal to zero to find critical values, and then test the quantity that you want to maximize at the critical values and at the endpoints of the interval. (recall that zn lies between x and c, x being the value that you are trying to approximate the function at and c being the value that the Taylor series is expanded about) The zn that yeilds the largest answer in absolute max/min test will be the value that should be substituted into the (n+1)st derivative of f.
evaluated at x = 1.) The term on the right hand side of this inequality, the Taylor remainder term, needs to be maximized so that we know what the largest possible error would be. How do you maximize any quantity? You find its derivative, set it equal to zero to find critical values, and then test the quantity that you want to maximize at the critical values and at the endpoints of the interval. (recall that zn lies between x and c, x being the value that you are trying to approximate the function at and c being the value that the Taylor series is expanded about) The zn that yeilds the largest answer in absolute max/min test will be the value that should be substituted into the (n+1)st derivative of f.
So for this example, to maximize the product 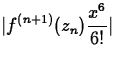 , we can maximize g(z) = |f(n+1)(z)| with respect to z over the interval
, we can maximize g(z) = |f(n+1)(z)| with respect to z over the interval ![]() by applying the absolute max/min test to g(z) and we would have to substitute our only x value, x=1, into
by applying the absolute max/min test to g(z) and we would have to substitute our only x value, x=1, into ![]() .
.
The following maple commands show the procedure in verifying the error bound.
> f := x -> sin(x); > g := z -> (D@@6)(f)(z); > a := diff(g(z),z); > b := fsolve(a = 0,z);
Notice that the critical value lies outside the interval in question, so we only need to evaluate f(6)(z) = g(z) = -sin z for the endpoints, z=0 and z=1.
> g(0); > evalf(g(1));
So, the maximum in absolute value would be 0.8414709848
and this is the z that we can substitute into ![]() .
.
Solution:
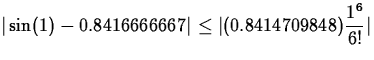
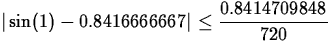
![]()
![]()
![]()
Note that this means that ![]() is accurate to three decimal places. Remember, that you were guaranteed accuracy to at least two decimal places.
is accurate to three decimal places. Remember, that you were guaranteed accuracy to at least two decimal places.
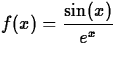 about x=0 that will give an error no greater than 0.05 over the interval
about x=0 that will give an error no greater than 0.05 over the interval Christine M Palmer