$next$ $up$ $previous$
Next: About this document ... Up: No Title Previous: No Title

Numerical Techniques - Integration and
Solving Equations

Purpose

Numerical techniques play a key role in computations, and Maple offers a variety of means for their performing. The present lab is composed in order to concentrate on the computational tools rather than on mathematical issues. Trying to make your knowledge of Maple more systematic, the lab pursues the following goals:

(i): to familiarize you with various Maple tools for numerical solving of equations and evaluating of definite integrals;
(ii): to provide you with basic experience in working with Maple as programming language.

Structure

This lab consists of two major parts - Background and Exercises. In the first, the relevant theoretical notes and description of the use of appropriate Maple commands and procedures are given. The second part includes four problems devoted to different numerical methods and various tools of Maple.

Background

Theoretical Notes

We know simple formulas for solving linear and quadratic equations, and there are more complicated formulas for cubic and quartic equations (equations of degree three and four). At one time it was hoped that similar formulas might be found for quintic and higher degree equations, but Niels Abel (a great Norwegian mathematician of the beginning of 19th century) showed that no formulas like these are possible for polynomial equations of degree greater than 4.

When exact formulas for solving an equation f(x) = 0 are not available, we can turn to numerical techniques from Calculus to approximate the solutions we seek. Two techniques considered in the course (the Bisection Method and Newton's method) are the examples of an idea of successive approximations allowing to localize the point (i.e., solutions, or roots) where the graph of y = f(x) passes through zero.

The idea of the Bisection Method is simple. If we know that a zero exists in the closed interval [a, b], the zero must lie in the sub-interval [a, (a+b)/2], or [(a+b)/2, b]. From the sign of f[(a+b)/2], we can determine which interval contains the zero. By repeatedly bisecting the interval, we can ``close in" on the zero of the function.

Newton's Method is based on the idea of using tangent lines to replace the graph of y = f(x) near the points where f is zero. The initial estimate x₀ may be found by graphing or just plain guessing. The method then uses the tangent to the curve y = f(x) at (x₀, f(x₀)) to approximate the curve, calling the point where the tangent meets the x-axis x₁. The number x₁ is usually a better approximation to the solution than x₀ is. The point, x₂, where the tangent to the curve at (x₁, f(x₁)) crosses the x-axis, is the next approximation in the sequence. We continue using each approximation to generate the next, until we are close enough to the root to stop.

Convergence of the Bisection Method is an almost obvious issue. The required accuracy can be initially chosen, and the iterations stop at step n when the error becomes less than (or equal to) the interval's half-length, i.e.:
$\begin{maplelatex} \begin{displaymath} \mid E_n\mid \leq h_n, \mbox{ where }h_n = \displaystyle\frac{b_n - a_n}{2}.\end{displaymath}\end{maplelatex}$
where a_n and b_n are the left and right points of the interval at the nth step respectively.

For Newton's approach, the convergence is not so obvious; moreover, the method does not always lead to convergence and requires an appropriate analysis (see Theorem A in Section 10.4 of the text). In practice, Newton's Method usually converges with impressive speed, but since this is not guaranteed one must test that convergence is actually taking place. The relevant tool for this testing is a sufficient condition of convergence establishing that the method converges to zero of f if
$\begin{maplelatex} \begin{displaymath} \left\vert\displaystyle\frac{f(x)f^{\prime\prime}(x)}{[f^\prime(x)]^2}\right\vert < 1\end{displaymath}\end{maplelatex}$
on an open interval containing the root.

Another important application of numerical techniques is integration. We may be unable to evaluate an integral (because of the absence of an antiderivative in terms of elementary functions) or desire to compose a procedure for a computer or calculator to evaluate definite integrals. Whatever the reason, we turn to numerical methods such as the Trapezoidal Rule and Simpson's Rule.

These methods actually estimate the area under a curve y = f(x) on the interval [a,b]. The accuracy of the entire procedure depends on how well the upper boundary of each approximating sub-region fits the shape of the given curve. It is clear, therefore, that trapezoids often result in a better approximation than rectangles (recall the geometric interpretation of the Riemann Sum), and Simpson's Rule using parabolic arcs for its upper boundaries provides a better approximation than trapezoids.

To approximate 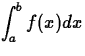$\displaystyle\int^b_a f(x)dx$ with the use of the Trapezoidal Rule, we apply the formula:
$\begin{maplelatex} % latex2html id marker 62 \begin{equation} T_n = \displaystyl... ... 2f(x_1) + 2f(x_2) +\ldots + 2f(x_{n-1}) + f(x_n)]\end{equation}\end{maplelatex}$

There is also an error term that can be used to estimate the error. More precisely, we have:
$\begin{maplelatex} % latex2html id marker 69 \begin{equation} \displaystyle\int^b_a f(x)dx = T_n + E_n \end{equation}\end{maplelatex}$
where
$\begin{maplelatex} % latex2html id marker 73 \begin{equation} \mid E_n\mid \leq ... ...laystyle\frac{(b-a)^3 f^{\prime\prime}(c)}{12n^2} \end{equation}\end{maplelatex}$
for some point c between a and b, provided $f^{\prime\prime}(c)$ exists on [a,b].

To approximate the definite integral by Simpson's Rule, the following formula is used:
$\begin{maplelatex} % latex2html id marker 80 \begin{equation} S_n = \displaystyl... ...)+4f(x_3)+\ldots +2f(x_{n-2})+4f(x_{n-1})+f(x_n)] \end{equation}\end{maplelatex}$

An error control in Simpson's Rule term is established through the analysis of the term E_n in (2) that now is specified as
$\begin{maplelatex} % latex2html id marker 88 \begin{equation} \mid E_n\mid \leq \displaystyle\frac{(b-a)^5 f^{(4)}(c)}{180n^4}\end{equation}\end{maplelatex}$
where, again, $a\leq c\leq b$ .

Maple Commands

There is a number of ways to implement the numerical techniques noted above working with Maple. In the present lab, you have to check out some of them; particularly, the special Maple commands directly implementing these methods and the procedures composed with the element of Maple programming means.

Maple is a very powerful computation system, so it is nothing surprising that many popular numerical procedures can be run just by a single command. In fact, some tools for solving equations were already in use in your previous labs. Here is a brief generalized review of these tools.

Maple has two commands for solving equations, solve and fsolve, providing exact and approximate solutions respectively. For example, to solve the quadratic equation
$\begin{maplelatex} \begin{displaymath} x^2 + 2x - 1 = 0,\end{displaymath}\end{maplelatex}$
we may either use

  > sol1 := solve(x^2+2*x-1=0,x);

$\begin{maplelatex} \begin{displaymath} \mbox{sol}1 := - 1 + \sqrt{2}, - 1 -\sqrt{2}\end{displaymath}\end{maplelatex}$
or label the left side of the equation by:

  > f := x^2=2*x-1:

  > sol2 := solve(f=0,x);

$\begin{maplelatex} \begin{displaymath} \mbox{sol}2 := - 1 + \sqrt{2}, - 1 -\sqrt{2}\end{displaymath}\end{maplelatex}$
or assign a variable name to the entire equation entering:

  > eq1 := x^2+2*x-1=0:

  > solve(eq1,x);

$\begin{maplelatex} \begin{displaymath} - 1 + \sqrt{2}, - 1 - \sqrt{2}\end{displaymath}\end{maplelatex}$
More than one equation can be solved by using curly brackets { }. For example:

  > eq_a := 3*x+2*y=1;

  > eq_b := x+2*y=3;

  > solve({eq_a,eq_b}, {x,y});

However, many equations cannot be solved exactly. If you forget Abel's Theorem and try finding the exact solutions to any polynomials of 5th degree or higher, you will encounter something like that:

  > eq2 := x^7+3*x^4+2*x-1=0:

  > solve(eq2,x);

$\begin{maplelatex} \begin{displaymath} \mbox{RootOf}(\_Z^7 + 3\_Z^4 + 2\_Z - 1)\end{displaymath}\end{maplelatex}$

Maple's response indicates that it does not know how to solve this equation exactly. In this situation, use fsolve command:

  > fsolve(eq2,x);

$\begin{maplelatex} \begin{displaymath} 0.4414177090\end{displaymath}\end{maplelatex}$

It is wise to use the fsolve command in conjunction with a plot in order to catch other solutions which may exist. Consider an equation:

  > eq3 := x^2+1/x-1/x^2=0:

  > fsolve(eq,x);

$\begin{maplelatex} \begin{displaymath} -1.220744085\end{displaymath}\end{maplelatex}$

However, the command:

  > plot(x^2+1/x-1/x^2, x=-3..3, y=-20..20);

shows that there is another branch of the graph of this function, and it crosses the x-axis at the point near 0.7. (Check it!) The second root can be found with the fsolve command but with modification indicating where we are looking for the root:

  > fsolve(eq,x,x=0..1);

$\begin{maplelatex} \begin{displaymath} 0.7244919590\end{displaymath}\end{maplelatex}$

Generally, fsolve find all the roots, however, some more complicated equations should be handled by a plot together with specifying a range with the fsolve command.

Maple can be used to plot an equation, but in this case the implicitplot command must be used instead of plot. In order to use this command, first load the plots package with the command

  > with(plots);

Try the implicitplot command to plot a circle using an equation of a circle.

In order to conduct computation using Eqs. (1) and (3), it might be useful to enter the general equation of the function and then find its value in various points by substitution (command subs).

Maple Procedures

It is clear from the conceptual description of the methods above (see the text, Sections 10.3 and 10.4), that they can provide reasonable closeness to the exact value if the number of approximating strips is large enough. Obviously, such processes as partition and successive computations in the Trapezoidal and Simpson's Method and iterations in the Bisection and Newton's Methods could be algorithmized and ordered to a computer. Actually, the solve and fsolve Maple commands are nothing but the built-in procedures involving sets of simple operations/commands and implementing such algorithms.

Maple possesses appropriate means which allow one to repeat some particular commands or set of commands many times with slightly different values; a number of commands could be gathered in an automating procedure. In this capacity, Maple reveals its features common for programming languages. The relative simplicity of the algorithms related to the numerical methods studying in this lab suggests the idea to introduce you to the elements of programming in Maple on the example of these methods.

To repeat a command you can compose a looping structure using the for and do commands. For example, the structure

  > for k from 1 by 0.5 to 3

               do
                 print (k, k^2);
               od;

prints out 5 pairs of numbers. Notice that the index moves from 1 to 3 by step 0.5. You may drop a portion by 0.5; in this case, the default value of the increment, that is 1, will be used and thus just three pairs will be printed. The command that is repeatedly performed is a print command and it is enclosed in the pair do/od (od is do in reverse).

To type this structure, press Shift + Enter in order to move the cursor to next line without executing the line. When you press enter at the end of the last line, all the lines will be performed, causing 5 (or 3) pairs of numbers to be displayed.

You can use this looping structure as part of a procedure:

  > maketable :=

               proc(n)
               for k from 1 by 0.5 to n
                 do
                   print (k, k^2);
                 od;
               end;

Remember to press Shift + Enter at the end of every line but the last as you enter this procedure. The procedure maketable uses n as its argument. Press Enter to define this procedure. Only a compact version of the procedure definition is displayed. Do not be concerned if a warning appears on the screen.

To use this procedure later, just type:

  > maketable(7);

$\begin{maplelatex} \begin{displaymath} \begin{array} {lll} &1 & 1\\ &1.5 & 2.2... ...9.00\\ &3.5 & 12.25\\ &4.0 & 16.00\end{array}\end{displaymath}\end{maplelatex}$

As you might expect, a table of squares of 7 numbers is displayed.

The loop is one of the two most basic constructs in programming. The other one is the if or conditional statement. It arises in many contexts. For example, you can use the if statement to implement an absolute value function:
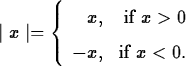
$\begin{maplelatex} \begin{displaymath} \mid x \mid = \left\{\begin{array} {rr} x... ...0\\ -x, &\mbox{if } x < 0.\end{array}\right.\end{displaymath}\end{maplelatex}$

Maple executes the if statement as follows: if x < 0, then Maple calculates -x; otherwise, it calculates x.

The procedure Abs to compute the absolute value function is shown below. The closing word fi (if in reverse) completes the if statement. In either case, the absolute value of x is the last result that Maple computes and so is the value that Abs returns.

  > Abs :=

             proc(x)
               if x < 0 then
                 -x;
               else
                 x;
               fi;
             end;

  > Abs(3); Abs(-2.3);

                                      3
                                     2.3

Notice that the portion else x can be dropped.

Some specific commands usually appear in connection with procedures. Command local specifies variables whose values Maple knows only inside the procedure; these are called local variables. While Maple executes a procedure, a global variable by the same name remains unchanged. Command type (a, *) checks the type of a variable a; some key word is used as *; for example, integer, even, equation, etc.

The syntax of all these commands is quite clear; additional information is available through Maple Help.

Exercises

Problem 1

Find the equation of the parabola that passes through the points (-1,2), (1,-1.5), and (4,7).

Problem 2

Here is a Maple source code for a non-standard procedure implementing Newton's Method.
Note: You may avoid typing the procedure by using the Getting Started Worksheet attached tothis lab. The text for the Newton Procedure is there.

  > Newton := proc (f, a, b, iter)

                local first, second, x, i, d1;
                if not type (f, procedure) then
                   ERROR ('the first argument must be a function name.') fi;
                if nargs <> 4 then ERROR ('You need four arguments.') fi;
                if evalf(f(a)*f(b)) >= 0 then
                   print ('f(a) and f(b) do not have opposite signs.');  
                fi;

                first := evalf((a+b)/2,15);
                print ('Initial estimate', evalf(first));
                d1 := diff(f(x), x);
                second := first - evalf(f(first)/subs(x=first, d1), 15);
                for i from 2 to iter 
                  do
                     first := second;
                     print (i - 1, evalf(first(f(first)/subs(x=first, d1), 15);
                  od;
                  print ('Final estimate', evalf(second));   
             end;

(a): Analyze the code. Explain how the iteration scheme of Newton's Method is implemented in it. Express plausible hypotheses about the nature of the particular cases handled by if statements with text outputs.
(b): Consider function $f(x) = \sin x - x + 1$ and find its root(s) using the commands solve and fsolve. Is the answer the same? Why?
(c): For the function in (b), apply the Newton procedure. Compare the result with (b). How many iterations did you need to get the root with nine digits of accuracy?
(d): Repeat points (b) and (c) for the function f(x) = x³ - 3x + 1. Illustrate your solution by plotting the function.

Problem 3

Find the area under the curve f(x) = e^-x² between 0 and 2 using the formula of the Trapezoidal Rule (1) with n = 4 and 8. Evaluate the corresponding integral by Maple tools. Compare the results and specify the number of decimal places that are correct in the approximate results.

Problem 4

Here is a Maple source code for a non-standard procedure implementing Simpson's Method.
Note: You may avoid typing the procedure by using the Getting Started Worksheet attached tothis lab. The text for the Newton Procedure is there.

  > Simpson := proc(f, a, b, n)

       local i, j, h, s, v;
       if not type(f, procedure) then
         ERROR ('the first argument must be a function name.') fi;
       if nargs <> 4 then ERROR ('You need four arguments.') fi;
       if (n mod 2 <> 0) then ERROR ('# of subdivisions must be even.') fi;
       h := (b-a)/n;
       for i from 1 to (n-1) 
         do
           v[i] := a + i*h;
         od;
       s := f(a) + f(b);
       for i from 1 by 2 to (n-1) 
         do
           s := s + 4*f(v[i]);
         od;
       for j from 2 by 2 to (n-2) 
         do
           s := s + 2*f(v[j]);
         od;

       s := (h/3) * s;
       evalf(s, 15);
    end;

[(a)] Analyze the code. Explain how the algorithm of the Simpson's Method is implemented in it. Express plausible hypotheses about the nature of the particular cases handled by if statements with text outputs.

[(b)] We know that
$\begin{maplelatex} \begin{displaymath} \displaystyle\int^1_0 \displaystyle\frac{4}{x^2 + 1}dx = 4[\arctan(1) - \arctan(0)] = \pi\end{displaymath}\end{maplelatex}$
Use the Simpson procedure with 4 different n (the highest value n = 40) to get 4 approximations for $\pi$ . Use your watch to estimate time required to perform each computation. Compare the results with the value of $\pi$ provided by Maple.

$next$ $up$ $previous$
Next: About this document ... Up: No Title Previous: No Title

Christine Marie Bonini
2/2/1999