
Suppose that D is a rectangular region in the the xy-plane, and that f(x,y) is a continuous, non-negative function on D. Then the volume of the solid above D and below z = f(x,y) is given by the double integral

We learned in class that such integrals can be evaluated by either of the iterated integrals
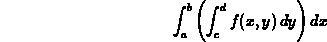
or
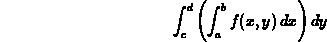
where the rectangle D is defined by the inequalities a < x < b and c < y < d.
Using Maple to evaluate double integrals proceeds in exactly the same fashion. For example, the following Maple commands show the computation of

for both orders of integration.
> int(int(x^2+y^2,x=-2..1),y=0..1);

> int(int(x^2+y^2,y=0..1),x=-2..1);

More complicated integrals are handled similarly. Suppose that we have f(x,y) = x2 + y2 and we want to know the volume of the solid between the region in the xy-plane bounded by the circle (x - 1)2 + y2 = 1 and the graph of f(x,y). Then an appropriate integral is
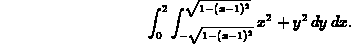
Using Maple, we calculate this as
> int(int(x^2+y^2,y=-sqrt(1-(x-1)^2)..sqrt(1-(x-1)^2)),x=0..2);

Computing triple integrals with Maple proceeds in a similar fashion. For example, the command to perform the following integral
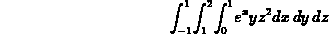
is
> int(int(int(exp(x)*y*z^2,x=0..1),y=1..2),z=-1..1);

It is sometimes helpful when you aren't sure you have the correct command to use the Int command, which is an inert form of the int command. Inert means that Maple just displays the integral and does not try to evaluate it. Here is an example.
> Int(Int(Int(exp(x)*y*z^2,x=0..1),y=1..2),z=-1..1);
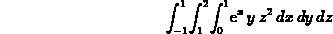
By using the inert Int command, you can easily check that the limits and the order of integration are correct.
More complicated triple integrals can also be done. For example, the volume of the region bounded by the paraboloid z = x2 + y2 and the plane z = y + 2 is given by the triple integral
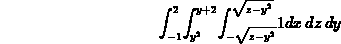
This integral can be computed with the following Maple command.
> int(int(int(1,x=-sqrt(z-y^2)..sqrt(z-y^2)),z=y^2..y+2),y=-1..2);

Maple can also be used to take some of the tedium out of calculations
of centroids, centers of mass, and moments of inertia.
Suppose that a mass with density function
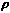 (x,y,z) = 1 - z/2
occupies the unit cube.
Then the following example shows how to compute the mass
and the coordinates of the center of mass of the body.
(x,y,z) = 1 - z/2
occupies the unit cube.
Then the following example shows how to compute the mass
and the coordinates of the center of mass of the body.
> mass := int(int(int(1-z/2,x=0..1),y=0..1),z=0..1);

> x_bar := int(int(int(x*(1-z/2),x=0..1),y=0..1),z=0..1)/mass;

> y_bar := int(int(int(y*(1-z/2),x=0..1),y=0..1),z=0..1)/mass;

> z_bar := int(int(int(z*(1-z/2),x=0..1),y=0..1),z=0..1)/mass;

Moments of Interia are computed in a similar fashion
using the definitions given in our text
(Varberg & Purcell, pp. 797-799).
Written by:
JDF
(E-Mail: bach@wpi.edu)
Last Updated: Friday, 6 October 2000
Copyright 2000, Joseph D. Fehribach