EXERCISES

1. Please use Maple to compute the volume between the region in the xy-plane bounded by the x-axis, the y-axis and the line x + y = 1, and the surface z = 8 - x² - y².
   
   
2. In both of the following text exercises, use Maple to compute the double integrals, and then sketch the region in the xy-plane over which the integral is defined.
   1. #7, p. 788
   2. #3, p. 793
   
   
3. Setup and evaluate first a double integral, then a triple integral to find the volume of the first octant part of the solid bounded by the cylinders x² + z² = 5 and y² + z² = 5. Also, generate a three-dimensional plot of the surface of the solid, something like this.
   
   
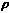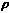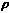4. Setup and evaluate a double integral to find I_z, the moment of inertia about the z-axis, of a lamina that covers the square in the plane with vertices (-1,-1), (1,-1), (1,1) and (-1,1), if the density is (x,y) = x²y²