


Next: About this document ...
Up: lab_template2
Previous: lab_template2
Subsections
The purpose of this lab is to acquaint you with using Maple to compute partial derivatives.
For a function 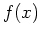 of a single real variable, the derivative
of a single real variable, the derivative
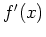 gives information on whether the graph of
gives information on whether the graph of 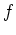 is increasing or decreasing. Finding where the derivative is zero was important in finding extreme values. For a function
is increasing or decreasing. Finding where the derivative is zero was important in finding extreme values. For a function 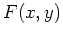 of two (or more) variables, the situation is more complicated.
of two (or more) variables, the situation is more complicated.
A differentiable function, 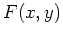 , of two variables has two partial
derivatives:
, of two variables has two partial
derivatives:
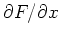 and
and
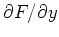 . As you have learned in class, computing partial derivatives is
very much like computing regular derivatives. The main difference is
that when you are computing
. As you have learned in class, computing partial derivatives is
very much like computing regular derivatives. The main difference is
that when you are computing
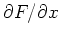 , you must treat
the variable
, you must treat
the variable 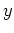 as if it was a constant and vice-versa when computing
as if it was a constant and vice-versa when computing
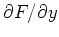 .
.
The Maple commands for computing partial derivatives are D
and diff. The diff command can be used on both expressions and functions whereas the D command can be used only on functions. The examples below show all first order and second order partials in Maple.
> f := (x,y) -> x^2*y^2-x*y;
> diff(f(x,y),x);
> diff(f(x,y),y);
> diff(f(x,y),x,x);
> diff(f(x,y),y,y);
> diff(f(x,y),x,y);
> D[1](f)(x,y);
> D[2](f)(x,y);
> D[1,1](f)(x,y);
> D[2,2](f)(x,y);
> D[1,2](f)(x,y);
The next example shows how to evaluate the mixed partial derivative of the function given above at the point 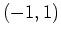 .
.
> der := diff(f(x,y),x,y);
> subs({x=-1,y=1},der);
> D[1,2](f)(-1,1);
The tangent plane like the tangent line to a single variable function is based on derivatives, however the partial derivatives are used for the tangent plane. Let's start with the equation of the tangent line to the function 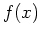 at the point where
at the point where 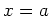 . Recall, the general equation of a line at the point
. Recall, the general equation of a line at the point 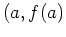 having slope
having slope 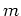 is
is
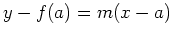 . This can be rewritten knowing that the derivative is the slope of a tangent line as
. This can be rewritten knowing that the derivative is the slope of a tangent line as
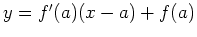 . Similarly for a funcion of two variables, the equation of the plane tangent to
. Similarly for a funcion of two variables, the equation of the plane tangent to 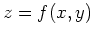 at the point
at the point 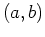 has the equation
has the equation
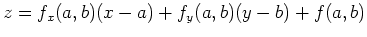 . The following example will show you how this can easily be translated to Maple syntax.
. The following example will show you how this can easily be translated to Maple syntax.
> g := x-> sin(x)-x^3/7+x^2;
> tanline := D(g)(5)*(x-5)+g(5);
> plot({g(x),tanline},x=-2..8);
The next example shows how to find the tangent plane to the function
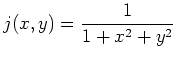 at
at 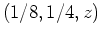 . You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff the subs command would be used.
. You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff the subs command would be used.
> f:=(x,y)->1/(1+x^2+y^2);
> tp:=D[1](f)(1/8,1/4)*(x-1/8)+D[2](f)(1/8,1/4)*(y-1/4)+f(1/8,1/4);
> plot3d({f(x,y),tp},x=-1..1,y=-1..1,style=patchnogrid);
To find a point where the tangent plane is horizontal, you would need to solve where both first order partials are equal to zero simultaneously.
> solve({diff(f(x,y),x)=0,diff(f(x,y),y)=0},{x,y});
- Given the single variable function
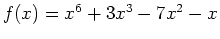
- a)
- Plot
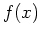 over the interval
over the interval
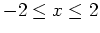 .
.
- b)
- Find the slope of
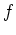 at
at 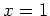 .
.
- c)
- Find another
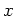 value that has the same slope as the slope at
value that has the same slope as the slope at 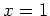 .
.
- d)
- Find the slope of the line containing the
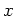 values from parts b and c.
values from parts b and c.
- e)
- Find the equation of a single line that is tangent to the graph of
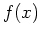 at both points from parts b and c snf plot the function and the tangent line on the same graph over the interval given in part a to show the line is tangent at both points.
at both points from parts b and c snf plot the function and the tangent line on the same graph over the interval given in part a to show the line is tangent at both points.
- Given:
- a)
- Find the tangent plane at
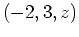 .
.
- b)
- Plot the function
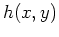 and the tangent plane over the intervals
and the tangent plane over the intervals
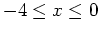 and
and
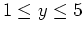 and rotate the plot so that you can see that the plane is tangent.
and rotate the plot so that you can see that the plane is tangent.
- There is only one point at which the plane tangent to the surface
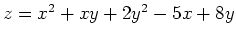 is horizontal. Find it and plot it along with the function on the same graph. Be sure to use axes so that you can rotate the graph and see that the tangent plane is horizontal.
is horizontal. Find it and plot it along with the function on the same graph. Be sure to use axes so that you can rotate the graph and see that the tangent plane is horizontal.



Next: About this document ...
Up: lab_template2
Previous: lab_template2
Dina Solitro
2006-09-18
![]() .
.
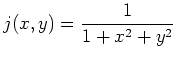 at
at ![]() . You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff the subs command would be used.
. You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff the subs command would be used.