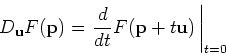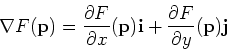Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
To assist you, there is a worksheet associated with this lab that
contains examples. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp /math/calclab/MA1024/Pardiff_grad_start.mws ~
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Pardiff_grad_start.mws, and go through it
carefully. Then you can start working on the exercises.
The graph of a function of a single real variable is a set of
points 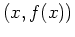 in the plane. Typically, the graph of such a
function
is a curve. For functions of two variables in Cartesian
coordinates, the graph is a set of points
in the plane. Typically, the graph of such a
function
is a curve. For functions of two variables in Cartesian
coordinates, the graph is a set of points 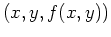 in
three-dimensional space. For this reason, visualizing
functions of two variables is usually more difficult. For stude
nts,
it is usually even more difficult if the surface is described in terms of polar or spherical coordinates.
in
three-dimensional space. For this reason, visualizing
functions of two variables is usually more difficult. For stude
nts,
it is usually even more difficult if the surface is described in terms of polar or spherical coordinates.
One of the most valuable services provided by computer software
such
as Maple is that it allows us to produce intricate graphs with
a minimum
of effort on our part. This becomes especially apparent when i
t comes
to functions of two variables, because there are many more comp
utations
required to produce one graph, yet Maple performs all these com
putations
with only a little guidance from the user.
The simplest way of describing a surface in Cartesian coordinates
is
as the graph of a function 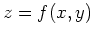 over a domain, e.g. a set
of
points in the
over a domain, e.g. a set
of
points in the 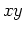 plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another way of representing a surface
plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another way of representing a surface 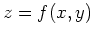 is through the use of level
curves. The idea is that a plane
is through the use of level
curves. The idea is that a plane 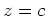 intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the 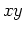 plane
is
called a level curve. A collection of such curves for different values
of
plane
is
called a level curve. A collection of such curves for different values
of 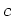 is a representation of the surface called a contour plot.
is a representation of the surface called a contour plot.
The partial derivatives
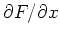 and
and
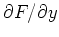 of
of 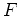 can be thought of as the rate of change of
can be thought of as the rate of change of 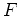 in
the direction parallel to the
in
the direction parallel to the 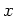 and
and 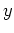 axes, respectively. The
directional derivative
axes, respectively. The
directional derivative
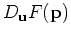 , where
, where
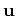 is a unit vector, is the rate of change of
is a unit vector, is the rate of change of 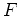 in the
direction
in the
direction 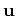 . There are several different ways that the
directional derivative can be computed. The method most often used
for hand calculation relies on the gradient, which will be described
below. It is also possible to simply use the definition
. There are several different ways that the
directional derivative can be computed. The method most often used
for hand calculation relies on the gradient, which will be described
below. It is also possible to simply use the definition
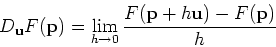
to compute the directional derivative. However, the following
computation, based on the definition, is often simpler to use.
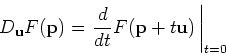
One way to think about this that can be helpful in understanding
directional derivatives is to realize that
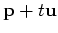 is
a straight line in the
is
a straight line in the  plane. The plane perpendicular to the
plane. The plane perpendicular to the
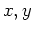 plane that contains this straight line intersects the surface
plane that contains this straight line intersects the surface 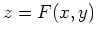 in a curve whose
in a curve whose 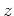 coordinate is
coordinate is
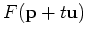 . The derivative of
. The derivative of
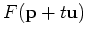 at
at 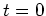 is the rate of change of
is the rate of change of 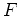 at
the point
at
the point 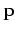 moving in the direction
moving in the direction 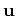 .
.
Maple doesn't have a simple command for computing directional
derivatives. There is a command in the tensor package that
can be used, but it is a little confusing unless you know something
about tensors. Fortunately, the method described above and the method
using the gradient described below are both easy to implement in
Maple. Examples are given in the Getting Started worksheet.
The gradient of 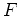 , written
, written 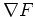 , is most easily computed as
, is most easily computed as
As described in the text, the gradient has several important
properties, including the following.
Maple has a fairly simple command grad in the linalg
package (which we used for curve computations). Examples of computing
gradients, using the gradient to compute directional derivatives, and
plotting the gradient field are all in the Getting Started
worksheet.
- Consider the following function.
- A)
- First, plot the graph of this function over the domain
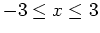 and
and
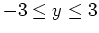 using the plot3d
command. Then use the
contourplot command to generate a contour plot of
using the plot3d
command. Then use the
contourplot command to generate a contour plot of 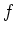 over the same domain having 20 contour lines.
over the same domain having 20 contour lines.
- B)
- What does the contour plot look like in the regions where the surface plot has a steep incline? What does it look like where the surface plot is almost flat?
- C)
- What can you say about the surface plot in a region whe
re the contour plot looks like a series of nested circles?
- Consider the function from exercise 1 which looks like a valley with a mountain opposite it. Is it p
ossible to find a path from the point
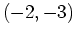 to
to
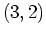 such that the valu
e of
such that the valu
e of 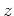 is always between
is always between 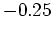 and
and 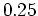 ? You do not have to
find a formula for your path, but you must present convincing evi
dence that it exists. For example, you might want to sketch your p
ath in by hand on an appropriate countour plot.
? You do not have to
find a formula for your path, but you must present convincing evi
dence that it exists. For example, you might want to sketch your p
ath in by hand on an appropriate countour plot.
- Consider again the function
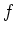 from the first exercise. Using
either method from the Getting Started worksheet, compute the
directional derivative of
from the first exercise. Using
either method from the Getting Started worksheet, compute the
directional derivative of 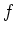 at the point
at the point 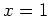 ,
, 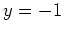 in the
three directions below.
in the
three directions below.
- A)
-
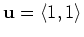
- B)
-
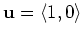
- C)
-
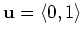
- Using the method from the Getting Started worksheet,
plot the gradient field and the contours of
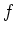 on the same plot. Use
the domain of
on the same plot. Use
the domain of
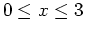 and
and
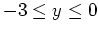 . Can you
use this plot to explain the values for the directional derivatives
you obtained in the previous exercises? By explaining the values, I
only mean can you explain what kind of surface it is and why the values were positive, negative, or
zero in terms of the contours and the gradient field?
. Can you
use this plot to explain the values for the directional derivatives
you obtained in the previous exercises? By explaining the values, I
only mean can you explain what kind of surface it is and why the values were positive, negative, or
zero in terms of the contours and the gradient field?



Next: About this document ...
Up: lab_template
Previous: lab_template
Jane E Bouchard
2007-09-17
![]() over a domain, e.g. a set
of
points in the
over a domain, e.g. a set
of
points in the ![]() plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another way of representing a surface
plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another way of representing a surface ![]() is through the use of level
curves. The idea is that a plane
is through the use of level
curves. The idea is that a plane ![]() intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the ![]() plane
is
called a level curve. A collection of such curves for different values
of
plane
is
called a level curve. A collection of such curves for different values
of ![]() is a representation of the surface called a contour plot.
is a representation of the surface called a contour plot.