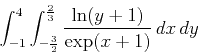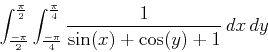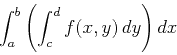
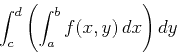
Following are examples of how to use
Maple to compute double integrals. It also has an example of how to
use Maple if the region of integration is of the more complicated form
![]() .
This is the case where the base of the solid is not rectangular, but
is bounded by two curves
.
This is the case where the base of the solid is not rectangular, but
is bounded by two curves ![]() and
and ![]() . If
. If ![]() is as
before, then the volume of the solid above
is as
before, then the volume of the solid above ![]() and below
and below ![]() is
given by
is
given by
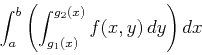
The main command for computing multiple integrals with Maple is the int command you are already familiar with. You simply use nested int commands and compute the integrals as iterated integrals.
To integrate a function over a rectangular region, just nest the two int commands. The following command computes the integral
![]()
>int(int(x^2+y^2,x=-2..1),y=0..1);This command computes the same integral, but in the opposite order. that is, it computes
>int(int(x^2+y^2,y=0..1),x=-2..1);Maple can also compute double intgrals where the limits are not constants. For example, suppose you wanted to compute the integral of
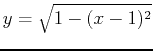 and
and
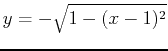 , which are just the upper and lower halves of the circle. The integral would be
, which are just the upper and lower halves of the circle. The integral would be
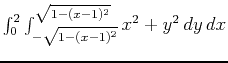 and the Maple command to do this integral is
and the Maple command to do this integral is
>int(int(x^2+y^2,y=-sqrt(1-(x-1)^2)..sqrt(1-(x-1)^2)),x=0..2);You can also use Maple to compute double integrals over regions that are x-simple. Suppose we repeat the previous calculation, but solve the equation for
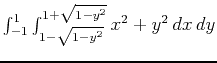 and the Maple command to do this is:
and the Maple command to do this is:
>int(int(x^2+y^2,x=1-sqrt(1-y^2)..1+sqrt(1-y^2)),y=-1..1);