Subsections

• Purpose
• Background
  • Locating Global Extrema
• Exercises

Finding and Classifying Extreme Values

Purpose

The purpose of this lab is to acquaint you with techniques for finding and classifying local and global extreme values of functions of two variables.

Background

Many applications of calculus involve finding the maximum and minimum values of functions. For example, suppose that there is a network of electrical power generating stations, each with its own cost for producing power, with the cost per unit of power at each station changing with the amount of power it generates. An important problem for the network operators is to determine how much power each station should generate to minimize the total cost of generating a given amount of power.

A crucial first step in solving such problems is being able to find and classify local extreme points of a function. What we mean by the term local extreme values is contained in the following definition.

Definition 349

Let f be a function defined at a point (x₀,y₀). Then f(x₀,y₀) is a local maximum if $f(x_0,y_0) \geq f(x,y)$ for all (x,y) in an open disk containing ( x₀,y₀) and f(x₀,y₀) is a local minimum if $f(x_0,y_0) \leq f(x,y)$ for all (x,y) in an open disk containing ( x₀,y₀). If f(x₀,y₀) is a local maximum or a local minimum, we say that it is a local extreme value.

In single-variable calculus, we found that the first derivative vanished at a local extreme value. For functions of two variables, both first-order partial derivatives vanish as described by the following theorem.

Theorem 355

If a function f has a local extreme value at a point (x₀,y₀) and the partial derivatives of f both exist at (x₀,y₀), then

$$\frac{\partial f}{\partial x}(x_0,y_0) = \frac{\partial f}{\partial y}(x_0,y_0) = 0$$

Notice that having both first order partial derivatives vanish means that the tangent plane is horizontal. Following the terminology we used for functions of a single variable, we call points where the partial derivatives f_x and f_y vanish critical points. Note carefully that the theorem does not say that a point where the partial derivatives vanish must be a local extreme point. Rather, it says that critical points are candidates for local extrema. Just as was the case for functions of a single variable, there can be critical points that are not extrema. For example, the saddle surface f(x,y) = x²-y² has a critical point at the origin, but it is not a local extremum.

Finding and classifying the local extreme values of a function f(x,y) requires several steps. First, the partial derivatives must be computed. Then the critical points must be solved for, which is not always a simple task. Finally, each critical point must be classified as a local maximum, local minimum, or neither. The following examples are intended to help you learn how to use Maple to simplify these tasks.

To compute partial derivatives in Maple, it is probably simplest to use the diff command. It is possible to use the D command for partial derivatives, but it is more complicated. The following examples show how to compute (in order) the partial derivatives f_x, f_y, f_xx, f_xy, and f_yy of the function $f(x,y) = exp(-x^2)\cos(y)$.

  > f := (x,y) -> exp(-x^2)*cos(y);

  > diff(f(x,y),x);

  > diff(f(x,y),y);

  > diff(f(x,y),x,x);

  > diff(f(x,y),x,y);

  > diff(f(x,y),y,y);

Finding critical points can often be accomplished by using the solve command, as shown below.

  > solve({diff(f(x,y),x) =0 ,diff(f(x,y),y) = 0},{x,y});

Notice that you have to give the solve command the set of equations to be solved and the set of variables to be solved for and that both sets have to be enclosed in curly braces.

The solve command doesn't always do the job. For example, it only reported two critical points above. It turns out, however, that the function has an infinite number to critical points of the form x=0, $y= n \pi$, where n is any integer. Having an infinite number of critical points often happens when trig functions are involved, so you need to watch out for it.

The solve command attempts to solve equations analytically. Unfortunately, there are some equations that just can't be solved analytically. When Maple can't solve a set of equations analytically, it gives no output from the solve command.s

If the solve command doesn't give the results you desire, there are alternatives. One possibility is to try to solve one of the equations for one of the variables in terms of the other, and then substitute into the other equation. This can work very well if it is easy to solve for one of the variables. Another, more general, method is to solve the equations numerically using the fsolve command. The main drawbacks are that the fsolve command only finds one solution at a time and that you usually have to have an idea of where the solution is. For example, if you attempt to use the fsolve command on our example without specifying where to look for the solution, Maple can't solve the equation, as shown below.

  > fsolve({diff(f(x,y),x) =0 ,diff(f(x,y),y) = 0},{x,y});

Error, (in fsolve/gensys) did not converge

On the other hand, we can solve for the critical point at x=0, $y=2\pi$ if we specify ranges for x and y containing the desired critical point as follows.

  > fsolve({diff(f(x,y),x) =0 ,diff(f(x,y),y) = 0},{x,y},
		x=-1..1,y=3.5..7);

Locating (if you have to use fsolve) and classifying critical points is probably best done with the plot3d command. By changing the plot ranges and using contours, you should be able to do this fairly easily.

Locating Global Extrema

In one-dimensional calculus, the absolute or global extreme values of a function occur either at a point where the derivative is zero, a boundary point, or where the derivative fails to exist. The situation for a function of two variables is very similar, but the problem is much more difficult because the boundary now consists of curves instead of just endpoints of intervals. For example, suppose that we wanted to find the global extreme values of a function f(x,y) on the rectangle $S = \{(x,y):\, a \leq x \leq b \mbox{ and } c \leq y \leq d\}$. The boundary of this rectangle consists of the four line segments given below.

$$\begin{array} {lcrc} y & = & c, & a \leq x \leq b \\ y & = &... ...a, & c \leq y \leq d \\ x & = & b, & c \leq y \leq d\end{array}$$

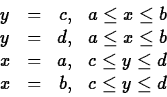
The basic theorem on the existence of global maximum and minimum values is the following.

Theorem 383

Suppose f(x,y) is continuous on a region S bounded by a simple closed curve, including the boundary. Then f(x,y) attains its absolute maximum value at some point (a,b) in S and absolute minimum value at some point (c,d) in S.

This theorem only says that the extrema exist, but doesn't help at all in finding them. However, we know that the global extrema occur either at local extrema, on the boundary of the region, or at points where one or the other partial derivative fails to exist. For example, to find the extreme values of a function f(x,y) on the rectangle given above, you would first have to find the interior critical points and then find the extreme values for the four one-dimensional functions

$$\begin{array} {lccc} g_1(x) & = & f(x,c), & a \leq x \leq b ... ...q y \leq d \\ h_2(y) & = & f(b,y), & c \leq y \leq d\end{array}$$

Exercises

1.

Describe the contours of a function near a critical point that is a local extremum. How do they differ from the contours near a critical point that is a saddle point? Give an example of each type.

2.

Find and classify the critical points for the following functions.

(a)

f(x,y) = x²-y².

(b)

$f(x,y) = \sin(x)\sin(y)$.

(c)

$f(x,y) = (1+x^2)\exp(-x^2-y^2)$.

3.

Consider the function

$$f(x,y) = \frac{x-y}{(3+x^2) (3+y^2)}$$

Find the absolute extrema of this function on the following domains.

(a)

The rectangle $-2 \leq x \leq 2$, $-2 \leq y \leq 2$.

(b)

The rectangle $0 \leq x \leq 2$, $0 \leq y \leq 2$.

(c)

The set of points in the plane satisfying x²/4+y² = 1. Note that if you want to plot a function f(x,y) over a region that is bounded by two curves y=g(x) and y=h(x) for $a \leq x \leq b$, the Maple plot3d command is

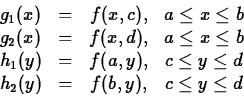
> plot3d(f(x,y),x=a..b,y=g(x)..h(x));

For more information, see the help page for plot3d

4.

What is the maximum possible volume of a rectangular box inscribed in a hemisphere of radius R? You may assume that one face of the box lies in the planar base of the hemisphere.