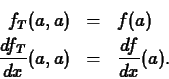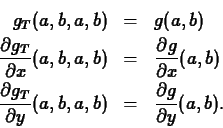Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with differentiating
multivariable functions.
You are already familiar with the Maple D and diff
commands for computing derivatives. These same commands can be used to
compute partial derivatives. As you have already learned, the
diff command is for differentiating Maple expressions and the
D command operates on functions. Examples are given below.
First, we define an expression.
>
p := x^2*sin(x*y);
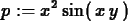
These commands compute
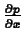 and
and
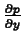 .
.
>
diff(p,x);
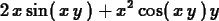
>
diff(p,y);
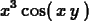
Higher order deriviatives are specified just by adding more
arguments. The following commands compute the mixed partial
derivatives
>
diff(p,x,y);
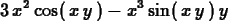
>
diff(p,y,x);
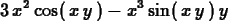
The D command can be simpler to use in some cases. However,
it only works on functions and you have to remember that the output of
the D command is also a function. Here are some examples.
>
f := (x,y) -> y*exp(x+y);
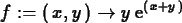
Here is
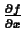 computed using the
diff command:
computed using the
diff command:
>
diff(f(x,y),x);
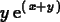
And the same thing using the D command:
>
D[1](f);
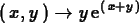
Here is the command for
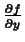
>
D[2](f);
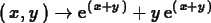
When you define a function of two or more variables in Maple, you
always have to provide names for the independent variables, and order
is important. In the case of the function 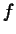 we defined above,
we defined above, 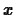 is
the first independent variable and
is
the first independent variable and 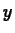 is the second. The D
command uses this order to specify partial derivatives. For example,
to find
is the second. The D
command uses this order to specify partial derivatives. For example,
to find
the syntax for the D command is as follows.
>
D[1,1](f);
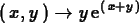
To obtain
use the following command.
>
D[1,2](f);
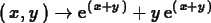
To obtain the expression corresponding to a partial derivative rather
than the function, use the following syntax. You can also use this
syntax to evaluate a partial derivative at a specific point.
>
D[1,2](f)(x,y);
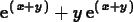
>
D[1,2](f)(0,1);
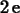
Definition 1
Suppose that
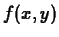
is differentiable at a point
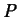
(see the text). Then
the gradient of
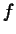
, denoted
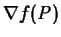
, is the vector
For example, if
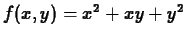 , then
, then
In Maple, you can calculate gradients using the grad command
in the linalg package.
>
with(linalg):
Warning: new definition for norm
Warning: new definition for trace
>
g := (x,y) -> x^2+x*y+y^2;
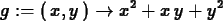
>
del_g := grad(g(x,y),[x,y]);
![\begin{maplelatex}
\begin{displaymath}
{\it del\_g} := [\,2\,{x} + {y}\,{x} + 2\,{y}\,]
\end{displaymath}\end{maplelatex}](img28.gif)
Note that the argument of grad is an expression and the output
is also an expression. Unfortunately, there is no elegant way to use the
output of grad as a function. The easiest way to evaluate
the gradient at a specific point is as follows:
>
subs(x=3,y=1,evalm(del_g));
![\begin{maplelatex}
\begin{displaymath}[\,7\,5\,]
\end{displaymath}\end{maplelatex}](img29.gif)
The evalm command is necessary when substituting into vectors. See what
happens without it.
The definition is straightforward to generalize to functions of three
or more independent variables - you just have as many components as
the number of independent variables. That is, for 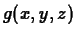 you would
have
you would
have
The Maple command for the gradient extends to this situation as well.
We know that
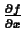 is the instantaneous
rate of change of
is the instantaneous
rate of change of 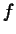 in the direction of the unit vector
in the direction of the unit vector 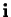 and
that, similarly,
and
that, similarly,
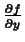 is the instantaneous
rate of change of
is the instantaneous
rate of change of 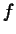 in the direction of the unit vector
in the direction of the unit vector 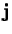 .
The gradient can be used to find the instantaneous rate of change in
other directions as follows.
.
The gradient can be used to find the instantaneous rate of change in
other directions as follows.
Definition 2
Suppose that
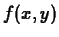
is differentiable at a point
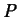
. Then for an
arbitrary unit vector
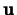
, the
directional derivative of
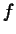
at
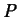
in the direction
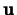
, denoted
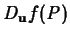
is
For example, let
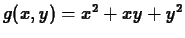 ,
, 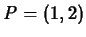 and
and
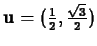 . Then we have
. Then we have
In Maple, computing directional derivatives can be a little clumsy, because
of the difficulties in substituting into the gradient. One way to calculate
a directional derivative is shown below.
>
with(linalg):
Warning: new definition for norm
Warning: new definition for trace
>
g := (x,y) -> x^2+x*y+y^2;
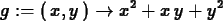
>
del_g := grad(g(x,y),[x,y]);
![\begin{maplelatex}
\begin{displaymath}
{\it del\_g} := [\,2\,{x} + {y}\,{x} + 2\,{y}\,]
\end{displaymath}\end{maplelatex}](img28.gif)
>
u := vector([1/2,sqrt(3)/2]);
![\begin{maplelatex}
\begin{displaymath}
{u} := \left[ \! \,{\displaystyle \frac {...
...ystyle
\frac {1}{2}}\,\sqrt {3}\, \! \right]
\end{displaymath}\end{maplelatex}](img41.gif)
>
r := subs({x=1,y=2},evalm(del_g));
![\begin{maplelatex}
\begin{displaymath}
{r} := [\,4\,5\,]
\end{displaymath}\end{maplelatex}](img42.gif)
Again, note the evalm command.
>
innerprod(r,u);
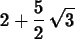
When we studied the calculus of functions of a single variable, we
used the derivative of a function 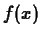 at a specific point
at a specific point 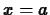 to
construct the linear approximation,
to
construct the linear approximation, 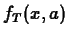 , given by the equation
, given by the equation
In the case of a function from 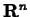 to
to 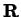 ,
, 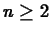 , we clearly have to do
something different because we have more than one independent
variable. As we will see below, it turns out that the linear
approximation is a function that is linear in each of the independent
variables. Thus, in the case of a function
, we clearly have to do
something different because we have more than one independent
variable. As we will see below, it turns out that the linear
approximation is a function that is linear in each of the independent
variables. Thus, in the case of a function 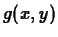 , we would expect
the linear approximation at a point
, we would expect
the linear approximation at a point 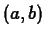 , denoted
, denoted 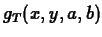 to
have the form
to
have the form
which is the equation of a plane.
Recall that the linear approximation of a scalar function satisfied the two
conditions
By analogy, you might expect the linear approximation to 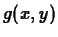 at a
point
at a
point 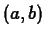 to satisfy the conditions
to satisfy the conditions
These turn out to be the correct conditions, and lead to the formula
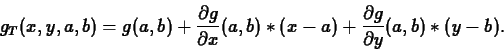 |
(1) |
A Maple procedure called TanPlane
is available in the CalcP package.
TanPlane outputs an expression that can be plotted or otherwise
manipulated. For example, you might want to plot it together with the
original function as shown below.
>
with(CalcP):
>
h := (x,y) -> x^2+y^2+2;
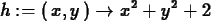
>
TanPlane(h(x,y),x=1,y=2);
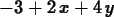
>
plot3d({h(x,y),TanPlane(h(x,y),x=1,y=2)},x=-5..5,y=-5..5);
- Compute the first and second order partial derivatives of the
function
Use Maple to plot the function and its first order partial
derivatives (not on the same plot).
- In the previous lab, you learned how to use the
contourplot command. Can you use a contour plot of a function
to obtain information about the gradient of the function? Illustrate
your answer by providing a contour plot of a function of your own
choosing on which you have drawn arrows at three points that represent
the gradient.
- Find the equations of the tangent planes for the following
functions at the specified points. Plot the graph of the function and
the tangent plane on the same plot. Be sure to choose a viewpoint and
a domain that best illustrates the relationship between the function and the
tangent plane.
-
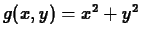 at
at 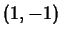 .
.
-
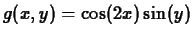 at
at 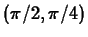 .
.
-
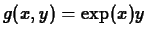 at
at 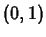 .
.
- Is there a way to use the tangent plane at a specific point to compute
the directional derivative at that same point? Show at least one
example to illustrate your answer.



Next: About this document ...
Up: lab_template
Previous: lab_template
William W. Farr
2000-12-01
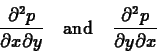
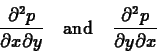
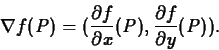
![]() you would
have
you would
have
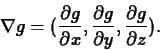
![]() is the instantaneous
rate of change of
is the instantaneous
rate of change of ![]() in the direction of the unit vector
in the direction of the unit vector ![]() and
that, similarly,
and
that, similarly,
![]() is the instantaneous
rate of change of
is the instantaneous
rate of change of ![]() in the direction of the unit vector
in the direction of the unit vector ![]() .
The gradient can be used to find the instantaneous rate of change in
other directions as follows.
.
The gradient can be used to find the instantaneous rate of change in
other directions as follows.
![]() ,
, ![]() and
and
![]() . Then we have
. Then we have
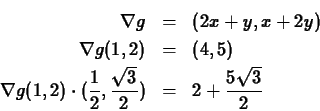
![]() to
to ![]() ,
, ![]() , we clearly have to do
something different because we have more than one independent
variable. As we will see below, it turns out that the linear
approximation is a function that is linear in each of the independent
variables. Thus, in the case of a function
, we clearly have to do
something different because we have more than one independent
variable. As we will see below, it turns out that the linear
approximation is a function that is linear in each of the independent
variables. Thus, in the case of a function ![]() , we would expect
the linear approximation at a point
, we would expect
the linear approximation at a point ![]() , denoted
, denoted ![]() to
have the form
to
have the form