


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with the application of local extreme values as it applies to the method of least-squares.
To assist you, there is a worksheet associated with this lab that
contains examples. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window, not in Maple.
cp /math/calclab/MA1024/Least_squares_start_B08.mws My_Documents
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Least_squares_start_B08.mws, and go through it
carefully. Then you can start working on the exercises.
Many applications of calculus involve finding the maximum and minimum
values of functions. For example, suppose that there is a network of
electrical power generating stations, each with its own cost for
producing power, with the cost per unit of power at each station
changing with the amount of power it generates. An important problem
for the network operators
is to determine how much power each station should generate to
minimize the total cost of generating a given amount of power.
A crucial first step in solving such problems is being able to find
and classify local extreme values of a function. What we mean by a
function 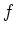 having a local extreme value at a point
having a local extreme value at a point 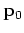 is
that for values of
is
that for values of 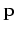 near
near 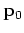 ,
,
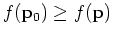 for a local maximum and
for a local maximum and
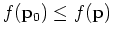 for a local minimum.
for a local minimum.
In single-variable
calculus, we found that we could locate candidates for local extreme
values by finding points where the first derivative vanishes. For
functions of two dimensions, the condition is that both first order
partial derivatives must vanish at a local extreme value candidate
point. Such a point is called a stationary point. It is also one of
the three types of points called critical points.
Note carefully that the condition does not say that a point where the partial
derivatives vanish must be a local extreme point. Rather, it says that
stationary points are candidates for local extrema. Just as was the case
for functions of a single variable, there can be stationary points that
are not extrema. For example, the saddle surface
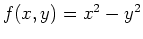 has a stationary point at the origin, but it is not a local extremum.
has a stationary point at the origin, but it is not a local extremum.
Finding and classifying the local extreme values of a function
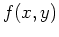 requires several steps. First, the partial derivatives must
be computed. Then the stationary points must be solved for, which is not
always a simple task.
requires several steps. First, the partial derivatives must
be computed. Then the stationary points must be solved for, which is not
always a simple task.
Next, one must check for the presence of
singular points, which might also be local extreme
values. Finally, each
critical point must be classified
as a local maximum, local minimum, or neither using the second-partials test
If
![$f_{xx}(a,b)f_{yy}(a,b)-[f_{xy}(a,b)]^2 >0 $](img9.png)
and
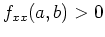
then
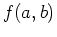
is a local minimum.
If
![$f_{xx}(a,b)f_{yy}(a,b)-[f_{xy}(a,b)]^2 >0 $](img9.png)
and
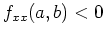
then
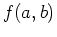
is a local maximum.
If
![$f_{xx}(a,b)f_{yy}(a,b)-[f_{xy}(a,b)]^2 <0$](img13.png)
then
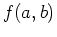
is a saddle point.
If
![$f_{xx}(a,b)f_{yy}(a,b)-[f_{xy}(a,b)]^2 =0$](img14.png)
then no conclusion can be made.
The least-squares method is based on the linear equation 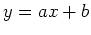 . Given data points, this method finds the equation of the line closest to all the data points. It does this by finding an a and b value such that the vertical distance to the least-squares line is a minimum. When the sum of all the distances squared is minimized, the result yields a slope and y-intercept of the line that best fits the data.
. Given data points, this method finds the equation of the line closest to all the data points. It does this by finding an a and b value such that the vertical distance to the least-squares line is a minimum. When the sum of all the distances squared is minimized, the result yields a slope and y-intercept of the line that best fits the data.
Notice that the function to be minimized is a function of two variables and therefore the second-partials test will be used.
The linear equation is not always the best fit for every set of data. We will look at a few other types of non-linear functions.
One example is the power law
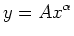 . Taking the natural log of both sides gives us a linear relationship between
. Taking the natural log of both sides gives us a linear relationship between 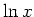 and
and 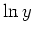 as follows:
as follows:
Another example is the exponential function
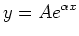 which again after taking the natural log of both sides results in a linear relationship between
which again after taking the natural log of both sides results in a linear relationship between 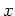 and
and 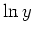 as follows:
as follows:
Given the data below, use the first column as data values for 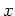 .
.
| X |
Y1 |
Y2 |
Y3 |
| 1 |
11.3 |
8.04 |
1.81 |
| 2 |
6.94 |
19.5 |
1.38 |
| 3 |
5.70 |
17.4 |
1.49 |
| 4 |
12.1 |
20.7 |
1.34 |
| 5 |
6.95 |
30.5 |
0.802 |
| 6 |
20.4 |
23.1 |
0.901 |
| 7 |
14.6 |
76.8 |
0.985 |
| 8 |
17.9 |
60.6 |
1.46 |
| 9 |
26 |
81.2 |
0.828 |
| 10 |
22.8 |
97.6 |
0.844 |
| 11 |
22.9 |
114 |
0.727 |
| 12 |
25.3 |
129 |
0.639 |
| 13 |
31 |
150 |
0.698 |
| 14 |
33.7 |
148 |
0.531 |
| 15 |
31.4 |
190 |
0.0482 |
| 16 |
34.2 |
193 |
0.510 |
| 17 |
25.5 |
212 |
0.378 |
| 18 |
38.7 |
225 |
0.471 |
| 19 |
38 |
247 |
0.292 |
| 20 |
44.9 |
270 |
0.360 |
- Use the second column as data values for
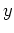 . Plot the data set
. Plot the data set 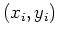 . Find the least-squares line that best fits the data and then plot the data set along with the least-squares line.
. Find the least-squares line that best fits the data and then plot the data set along with the least-squares line.
- Use the third column as data values for
 . Plot the data set
. Plot the data set 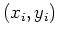 . Find a power-law function that best fits the data. Include a plot of the data set the corresponds to
. Find a power-law function that best fits the data. Include a plot of the data set the corresponds to
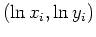 along with the least-squares line and also a plot of the original data set
along with the least-squares line and also a plot of the original data set 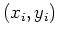 along with the power-law function that best fits the data.
along with the power-law function that best fits the data.
- Use the fourth column as data values for
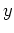 . Plot the data set
. Plot the data set 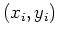 . Find an exponential funtion that best fits the data. Include a plot of the data set the corresponds to
. Find an exponential funtion that best fits the data. Include a plot of the data set the corresponds to 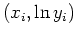 along with the least-squares line and also a plot of the original data set
along with the least-squares line and also a plot of the original data set 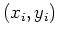 along with the exponential function that best fits the data.
along with the exponential function that best fits the data.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2008-11-24
![]() having a local extreme value at a point
having a local extreme value at a point ![]() is
that for values of
is
that for values of ![]() near
near ![]() ,
,
![]() for a local maximum and
for a local maximum and
![]() for a local minimum.
for a local minimum.
![]() has a stationary point at the origin, but it is not a local extremum.
has a stationary point at the origin, but it is not a local extremum.
![]() requires several steps. First, the partial derivatives must
be computed. Then the stationary points must be solved for, which is not
always a simple task.
requires several steps. First, the partial derivatives must
be computed. Then the stationary points must be solved for, which is not
always a simple task.
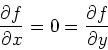
![\begin{displaymath}
f(a,b)=d_{1}^2+d_{2}^2+...+d_{n}^2=\sum_{i=1}^n[y_{i}-(ax_{i}+b)]^2
\end{displaymath}](img16.png)