


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory with the following command,
which must be run in a terminal window for example, not in Maple.
cp /math/calclab/MA1024/Coords_start_B11.mws ~/My_Documents
You can copy the worksheet now, but you should read through the lab
before you load it into Maple. Once you have read to the exercises,
start up Maple, load
the worksheet Coords_start_B11.mws, and go through it
carefully. Then you can start working on the exercises.
Defining surfaces with rectangular coordinates often times becomes more complicated than necessary. A change in coordinates can simplify things. The easiest examples are a sphere and a cylinder.
> with(plots):
> f1:=x^2+y^2+z^2=49;
> g1:=rho=7;
> implicitplot3d(f1,x=-7..7,y=-7..7,z=-7..7,axes=boxed,scaling=comstrained);
> implicitplot3d(g1,rho=0..7.5,theta=0..2*Pi,phi=0..Pi,coords=spherical,
numpoints=5000,axes=boxed);
> f2:=x^2+y^2=49;
> h2:=r=7;
> implicitplot3d(f2,x=-7..7,y=-7..7,z=-8..8,axes=boxed);
> implicitplot3d(h2,r=0..7.5,theta=0..2*Pi,z=-8..8,coords=cylindrical,
numpoints=3000,axes=boxed);
To change to cylindrical coordinates from rectangular coordinates use the conversion:
Where 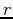 is the radius in the x-y plane and
is the radius in the x-y plane and 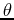 is the angle in the x-y plane.
To change to spherical coordinates from rectangular coordinates use the conversion:
is the angle in the x-y plane.
To change to spherical coordinates from rectangular coordinates use the conversion:
Where 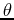 is the angle in the x-y plane;
is the angle in the x-y plane; 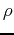 is the radius from the origin in any direction; and
is the radius from the origin in any direction; and 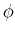 is the angle in the x-z plane.
As an example, the equation of an ellipsoid in rectangular coordinates is
is the angle in the x-z plane.
As an example, the equation of an ellipsoid in rectangular coordinates is
> f3:=x^2/23+y^2/23+z^2/122=1;
>implicitplot3d(f3,x=-5..5,y=-5..5,z=-12..12,scaling=constrained,axes=boxed);
Changing to sherical coordinates:
> g3:=simplify(subs({x=rho*sin(phi)*cos(theta),y=rho*sin(phi)*sin(theta),
z=rho*cos(phi)},f3));
> implicitplot3d(g3,rho=0..12,theta=0..2*Pi,phi=0..Pi,coords=spherical,axes=boxed,
scaling=constrained,numpoints=2000);
- Given the rectangular equation for a hyperboloid of one sheet:
- A)
- Graph the equation using the domain values of
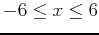 ,
,
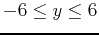 and the range values
and the range values
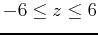 .
.
- B)
- Write the equation in cylindrical coordinates and then graph the equation.
- C)
- Write the equation in spherical coordinates and graph it.
- D)
- Looking at the three equations, which coordinates appears to give the simplest equation?
- Given the equation of a torus (a.k.a. donut):
Hint: In all graphs below, use
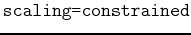 .
.
- A)
- Graph the equation using the domain values
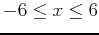 ,
,
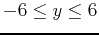 and the range values
and the range values
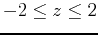 .
.
- B)
- Write the equation in cylindrical coordinates and graph it.
- C)
- Write the equation in spherical coordinates (hint: use the factor command outside the simplify command to simplify even more). Then graph your equation.
- D)
- Looking at the three equations, which coordinates appear to give the simplest equation?
- Last week, you proved that the volume of a sphere of radius
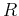 is
is
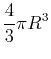 using a double integral. Prove this again using a triple integral in all 3 coordinate systems. Use uppercase
using a double integral. Prove this again using a triple integral in all 3 coordinate systems. Use uppercase 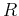 for the radius to distinguish from the variable
for the radius to distinguish from the variable 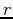 in cylindrical coordinates. Remember to use the command
in cylindrical coordinates. Remember to use the command
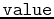 instead of
instead of
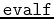 . If you had to calculate one of these triple integrals by hand, which one would be the simplest?
. If you had to calculate one of these triple integrals by hand, which one would be the simplest?



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2011-12-06
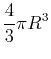 using a double integral. Prove this again using a triple integral in all 3 coordinate systems. Use uppercase
using a double integral. Prove this again using a triple integral in all 3 coordinate systems. Use uppercase