


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with using Maple to compute
partial derivatives.
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory by going to your computer's Start menu and choose run. In the run field type:
\\filer\calclab
when you hit enter, you can then choose MA1024 and then choose the worksheet
Pardiff_start_B13.mw
Remember to immediately save it in your own home directory. Once you've copied and saved the worksheet, read through the background on the internet and the background of the worksheet before starting the exercises.
For a function 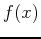 of a single real variable, the derivative
of a single real variable, the derivative
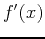 gives information on whether the graph of
gives information on whether the graph of 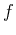 is increasing or
decreasing. Finding where the derivative is zero was important in
finding extreme values. For a function
is increasing or
decreasing. Finding where the derivative is zero was important in
finding extreme values. For a function 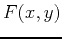 of two (or more)
variables, the situation is more complicated.
of two (or more)
variables, the situation is more complicated.
A differentiable function, 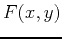 , of two variables has two partial
derivatives:
, of two variables has two partial
derivatives:
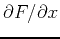 and
and
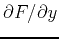 . As you have learned in class, computing partial derivatives is
very much like computing regular derivatives. The main difference is
that when you are computing
. As you have learned in class, computing partial derivatives is
very much like computing regular derivatives. The main difference is
that when you are computing
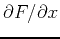 , you must treat
the variable
, you must treat
the variable 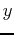 as if it was a constant and vice-versa when computing
as if it was a constant and vice-versa when computing
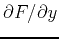 .
.
The Maple commands for computing partial derivatives are D
and diff. The Getting Started worksheet has examples
of how to use these commands to compute partial derivatives.
- Compute the three distinct second order partial derivatives of
at the point
 using the diff command and then again using the D command.
using the diff command and then again using the D command.
- Find the equation of the plane tangent to
at the point 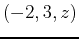 . Plot the function
. Plot the function 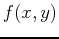 and the tangent plane over the intervals
and the tangent plane over the intervals
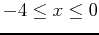 and
and
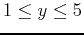 and rotate the plot so that you can see that the plane is tangent.
and rotate the plot so that you can see that the plane is tangent.
- Given the function
- a)
- Plot the function and the plane
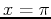 on the same graph. Use intervals
on the same graph. Use intervals
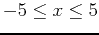 ,
,
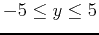 ,
,
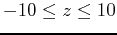 .
.
- b)
- Find the derivative of
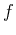 in the
in the 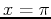 plane.
plane.
- c)
- Find the equation of the line tangent to the two-dimensional intersection of the plane
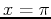 and
and 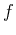 at the point
at the point 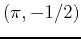 and plot them on the same graph.
and plot them on the same graph.
- d)
- Does your two-dimensional graph look like the intersection from your three-dimensional graph? Be sure to use the same ranges to properly compare and rotate the 3-D graph.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2013-11-10
 using the diff command and then again using the D command.
using the diff command and then again using the D command.
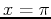 on the same graph. Use intervals
on the same graph. Use intervals
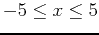 ,
,
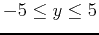 ,
,
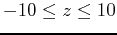 .
.
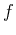 in the
in the 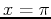 plane.
plane.
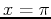 and
and 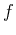 at the point
at the point 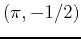 and plot them on the same graph.
and plot them on the same graph.